链表
# 链表
# 单向链表
# 动态数组的缺点
动态数组有个明显的缺点：
那就是可能会造成内存空间的大量浪费。（假设扩容了，但是只新增了一个元素，这就会导致后面的数组内存空间浪费）
能否用到多少就申请多少内存？
答案是可以的，链表就可以办到这一点。
- ArrayList 需要预先分配内存，设置默认容量
- LinkList 不需要预先分配内存，自然也不需要设置默认容量
# 链表简介
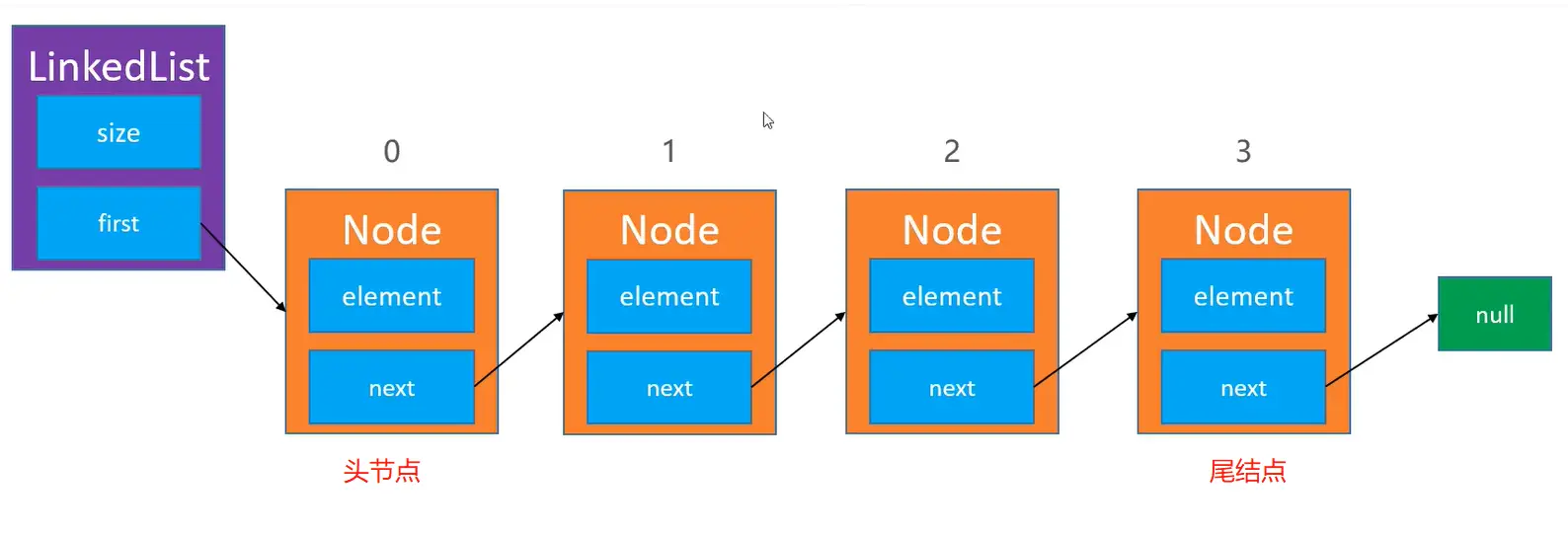
链表是一种链式存储的线性表，所有元素的内存地址不一定是连续的。
链表应该包含两样东西：size 和 first。
- size：代表你将来存储的多少个元素，相当于你有多少个节点，多少个 NODE。
- first：指向你的第一个元素，也就是头节点，第 0 个位置的节点。
# 接口设计
链表的大部分接口和动态数组是一致的。
# 接口类 List
首先可以抽象出一个接口类，方便代码的使用。（当做动态数组和链表的父类）
具体代码实现
public interface List<E> {
static final int ELEMENT_NOT_FOUND = -1;
/**
* 清除所有元素
*/
void clear();
/**
* 元素的数量
* @return
*/
int size();
/**
* 是否为空
* @return
*/
boolean isEmpty();
/**
* 是否包含某个元素
* @param element
* @return
*/
boolean contains(E element);
/**
* 添加元素到尾部
* @param element
*/
void add(E element);
/**
* 获取index位置的元素
* @param index
* @return
*/
E get(int index);
/**
* 设置index位置的元素
* @param index
* @param element
* @return 原来的元素ֵ
*/
E set(int index, E element);
/**
* 在index位置插入一个元素
* @param index
* @param element
*/
void add(int index, E element);
/**
* 删除index位置的元素
* @param index
* @return
*/
E remove(int index);
/**
* 查看元素的索引
* @param element
* @return
*/
int indexOf(E element);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
# 抽象类 AbstractList
抽象类不对外公开，并且是无法被 new 创建的。
- 抽象类可以编写一些公共代码（抽取类结构），而接口里面不能。
- 而且抽象类实现接口类时可以不用全部接口方法都实现。
当做父类，ArrayList 和 LinkList 都可以继承它。
具体代码实现
public abstract class AbstractList<E> implements List<E> {
/**
* 元素的数量
* 注意这里写的是protect，允许子类使用
*/
protected int size;
/**
* 元素的数量
* @return
*/
public int size() {
return size;
}
/**
* 是否为空
* @return
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 是否包含某个元素
* @param element
* @return
*/
public boolean contains(E element) {
return indexOf(element) != ELEMENT_NOT_FOUND;
}
/**
* 添加元素到尾部
* @param element
*/
public void add(E element) {
add(size, element);
}
protected void outOfBounds(int index) {
throw new IndexOutOfBoundsException("Index:" + index + ", Size:" + size);
}
protected void rangeCheck(int index) {
if (index < 0 || index >= size) {
outOfBounds(index);
}
}
protected void rangeCheckForAdd(int index) {
if (index < 0 || index > size) {
outOfBounds(index);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 单向链表 SingleLinkedList
代码实现：
public class SingleLinkedList<E> extends AbstractList<E> {
private Node<E> first;
private static class Node<E> {
E element;
Node<E> next;
public Node(E element, Node<E> next) {
this.element = element;
this.next = next;
}
}
@Override
public void clear() {
size = 0;
first = null;
}
@Override
public E get(int index) {
/*
* 最好：O(1)
* 最坏：O(n)
* 平均：O(n)
*/
return node(index).element;
}
@Override
public E set(int index, E element) {
/*
* 最好：O(1)
* 最坏：O(n)
* 平均：O(n)
*/
Node<E> node = node(index);
E old = node.element;
node.element = element;
return old;
}
@Override
public void add(int index, E element) {
/*
* 最好：O(1)
* 最坏：O(n)
* 平均：O(n)
*/
rangeCheckForAdd(index);
if (index == 0) {
first = new Node<>(element, first);
} else {
Node<E> prev = node(index - 1);
prev.next = new Node<>(element, prev.next);
}
size++;
}
@Override
public E remove(int index) {
/*
* 最好：O(1)
* 最坏：O(n)
* 平均：O(n)
*/
rangeCheck(index);
Node<E> node = first;
if (index == 0) {
first = first.next;
} else {
Node<E> prev = node(index - 1);
node = prev.next;
prev.next = node.next;
}
size--;
return node.element;
}
@Override
public int indexOf(E element) {
if (element == null) {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (node.element == null) return i;
node = node.next;
}
} else {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (element.equals(node.element)) return i;
node = node.next;
}
}
return ELEMENT_NOT_FOUND;
}
/**
* 获取index位置对应的节点对象
* @param index
* @return
*/
private Node<E> node(int index) {
rangeCheck(index);
Node<E> node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
}
@Override
public String toString() {
StringBuilder string = new StringBuilder();
string.append("size=").append(size).append(", [");
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (i != 0) {
string.append(", ");
}
string.append(node.element);
node = node.next;
}
string.append("]");
// Node<E> node1 = first;
// while (node1 != null) {
//
//
// node1 = node1.next;
// }
return string.toString();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
# 边界问题
在编写链表过程中，要注意边界测试，比如 index 为 0 、size – 0 、size 时
比如：添加(add)元素时，要注意 0 这个位置
# 练习
# 237.删除链表中的节点
地址：237. 删除链表中的节点 - 力扣（LeetCode） (opens new window)
题解：
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public void deleteNode(ListNode node) {
node.val = node.next.val;
node.next = node.next.next;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
# 206.反转链表 - 递归
地址：206. 反转链表 - 力扣（LeetCode） (opens new window)
用递归的方法
题解：
class Solution {
public ListNode reverseList(ListNode head) {
// 1、边界条件
if (head == null || head.next == null) {
return head;
}
// 2、递归调用 -- 从第2个节点开始反转
ListNode newhead = reverseList(head.next);
// 3、边界处理 -- 最后一个节点的逻辑处理（想想需求是什么）
head.next.next = head;
head.next = null;
// 4、返回递归结果
return newhead;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 应用递归的诀窍
首先得搞清楚这个递归方法的作用，然后充分利用它的作用去做事情就可以了。
总结四步骤：
- 定义边界条件
- 递归方法调用
- 边界逻辑处理
- 返回递归结果
# 206.反转链表 - 迭代
非递归解法
题解：
public ListNode reverseList(ListNode head) {
// 1、边界条件
if (head == null || head.next == null) {
return head;
}
ListNode newhead = null;
while (head != null) {
// 循环四步曲
ListNode tmp = head.next;
head.next = newhead;
newhead = head;
head = tmp;
}
return newhead;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
图解：
反转前
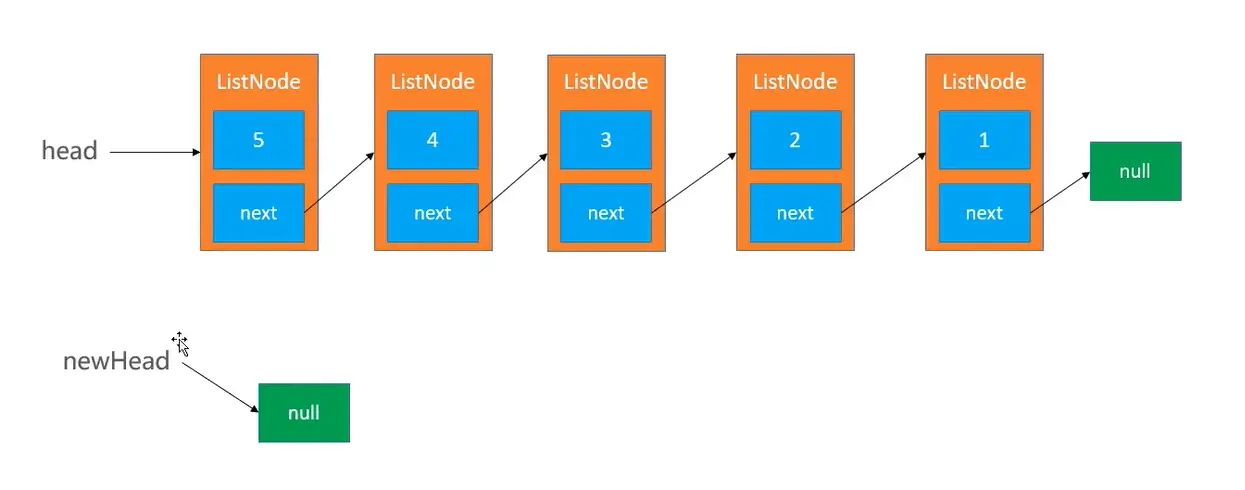
反转后
1、第 1 次循环
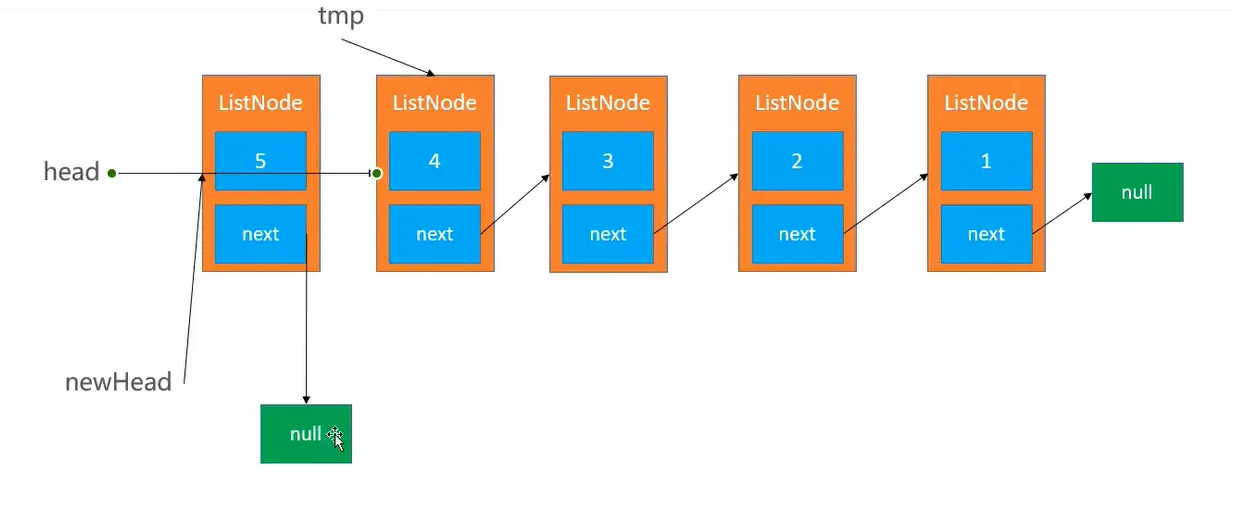
2、第 2 次循环
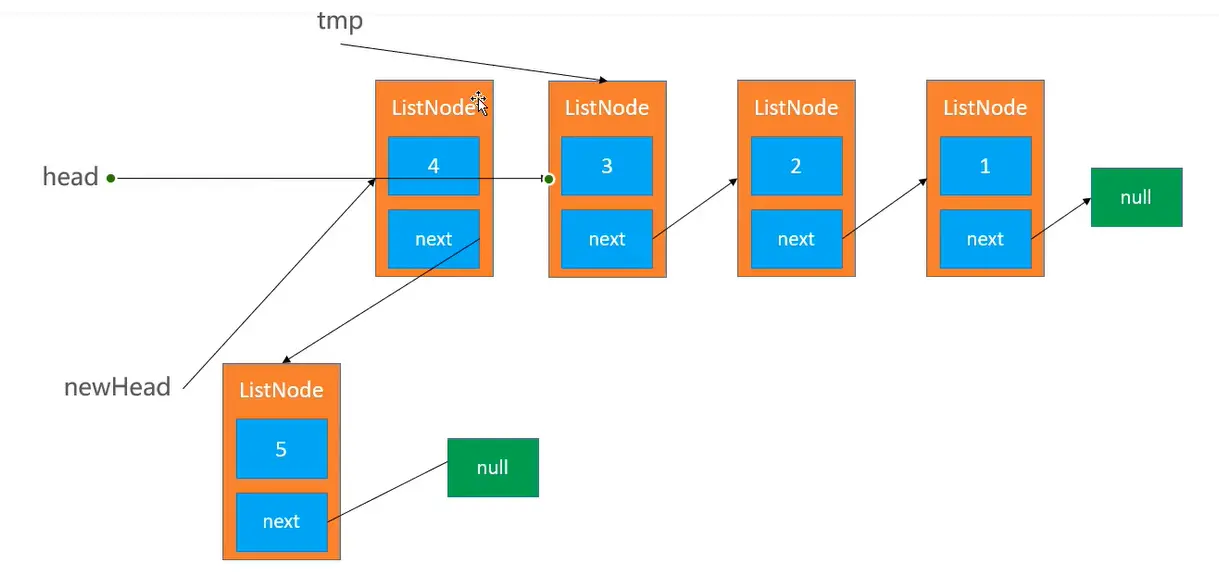
# 141.环形链表
地址：141. 环形链表 - 力扣（LeetCode） (opens new window)
题解：
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode fast = head.next;
ListNode slow = head;
while(fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) return true;
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
# 203.移除链表元素
地址：203. 移除链表元素 - 力扣（LeetCode） (opens new window)
1
# 83.删除排序链表中的重复元素
地址：83. 删除排序链表中的重复元素 - 力扣（LeetCode） (opens new window)
# 876.链表的中间结点
地址：876. 链表的中间结点 - 力扣（LeetCode） (opens new window)
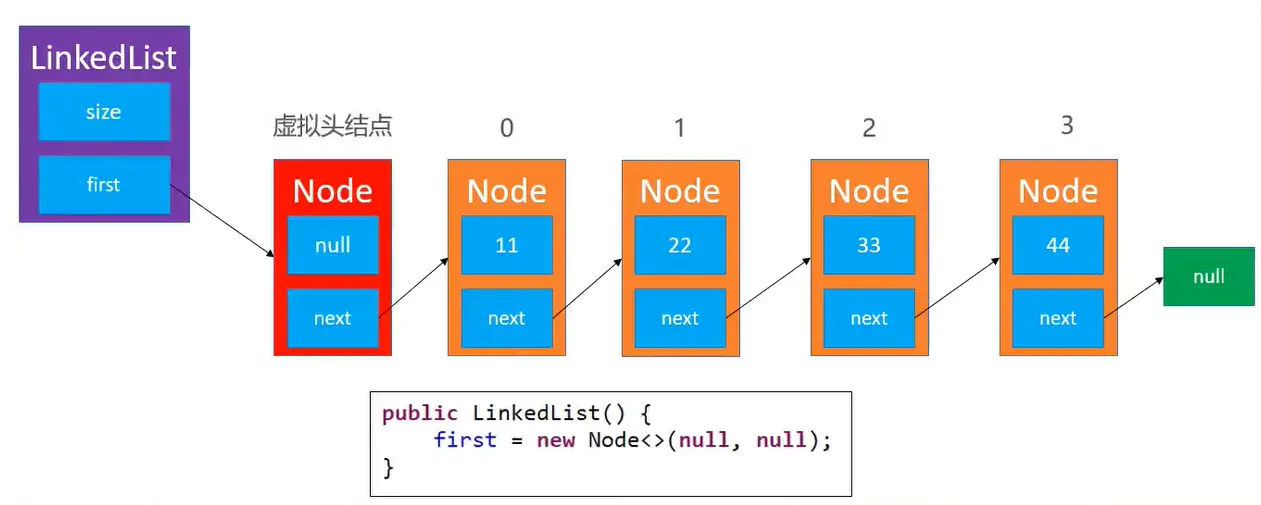
# 虚拟头节点
有时候为了让代码更加精简，统一所有节点的处理逻辑，可以在最前面增加一个虚拟的头结点(不存储数据)
但不建议加上这么一个虚拟头节点，因为这个也浪费内存，而且无缘无故多一个不存储任何数据的东西，会觉得挺别扭的。
# 为什么说链表的插入与删除复杂度是O(1)?
这里的 O(1) 是指插入与删除操作的那一刻是 O(1)。
但是整体的操作的复杂度还是 O(n) -- 要算上找元素的时间
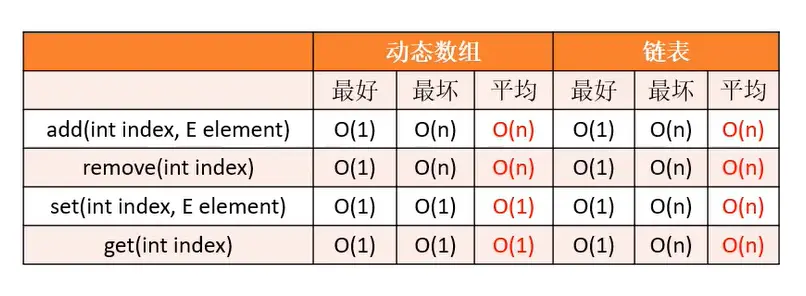
# 复杂度分析
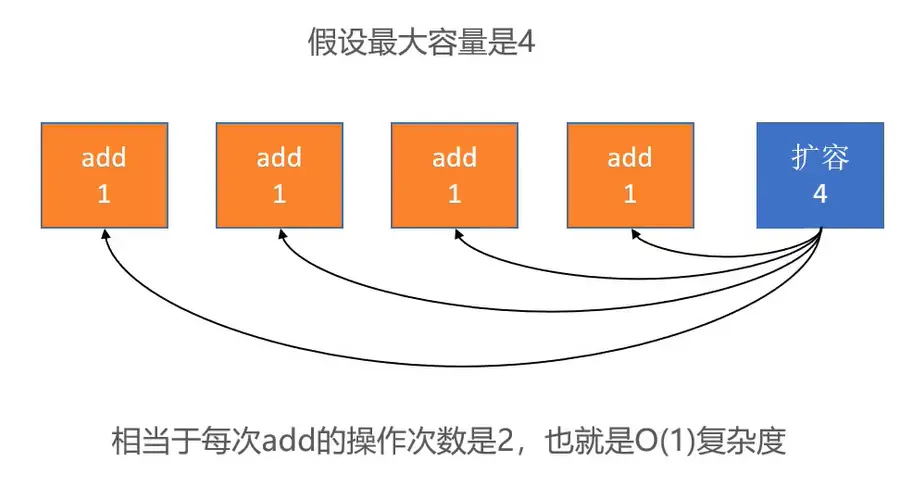
# 均摊复杂度
动态数组 add(E element) 复杂度分析
最好: O(1) 最坏: O(n) 平均: O(1) 均摊: O(1)
具体分析如下图所示：
什么情况下适合使用均摊复杂度呢？
当经过连续的多次复杂度比较低的情况后，出现个别复杂度比较高的情况下，就适合使用均摊复杂度。
# ArrayList 缩容
如果内存使用比较紧张，动态数组有比较多的剩余空间，可以考虑进行缩容操作。
比如剩余空间占总容量的一半时，就进行缩容。
1、添加 trim() 方法
private void trim() {
// 30
int oldCapacity = elements.length;
// 15
int newCapacity = oldCapacity >> 1;
if (size > (newCapacity) || oldCapacity <= DEFAULT_CAPACITY) return;
// 剩余空间还很多
E[] newElements = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newElements[i] = elements[i];
}
elements = newElements;
System.out.println(oldCapacity + "缩容为" + newCapacity);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2、在 remove 方法中调用
public E remove(int index) {
rangeCheck(index);
E old = elements[index];
for (int i = index + 1; i < size; i++) {
elements[i - 1] = elements[i];
}
elements[--size] = null;
trim(); // 判断是否缩容
return old;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
3、clear 清除元素的时候也需要缩容
/**
* 清除所有元素
*/
public void clear() {
for (int i = 0; i < size; i++) {
elements[i] = null; // 内存管理细节
}
size = 0;
// 缩容数值仅供参考
if (elements != null && elements.length > DEFAULT_CAPACITY) {
elements = (E[]) new Object[DEFAULT_CAPACITY];
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
# 复杂度震荡
如果扩容倍数、缩容时机设计不得当，有可能会导致复杂度震荡。
比如扩容倍数为 2，缩容时机为 1/2，两者相乘等于 1 的情况下。
扩容前复杂度为 O(1)，扩容时复杂度为 O(n)，突然从一个很低的复杂度变到一个很高的复杂度，就称它为复杂度震荡。
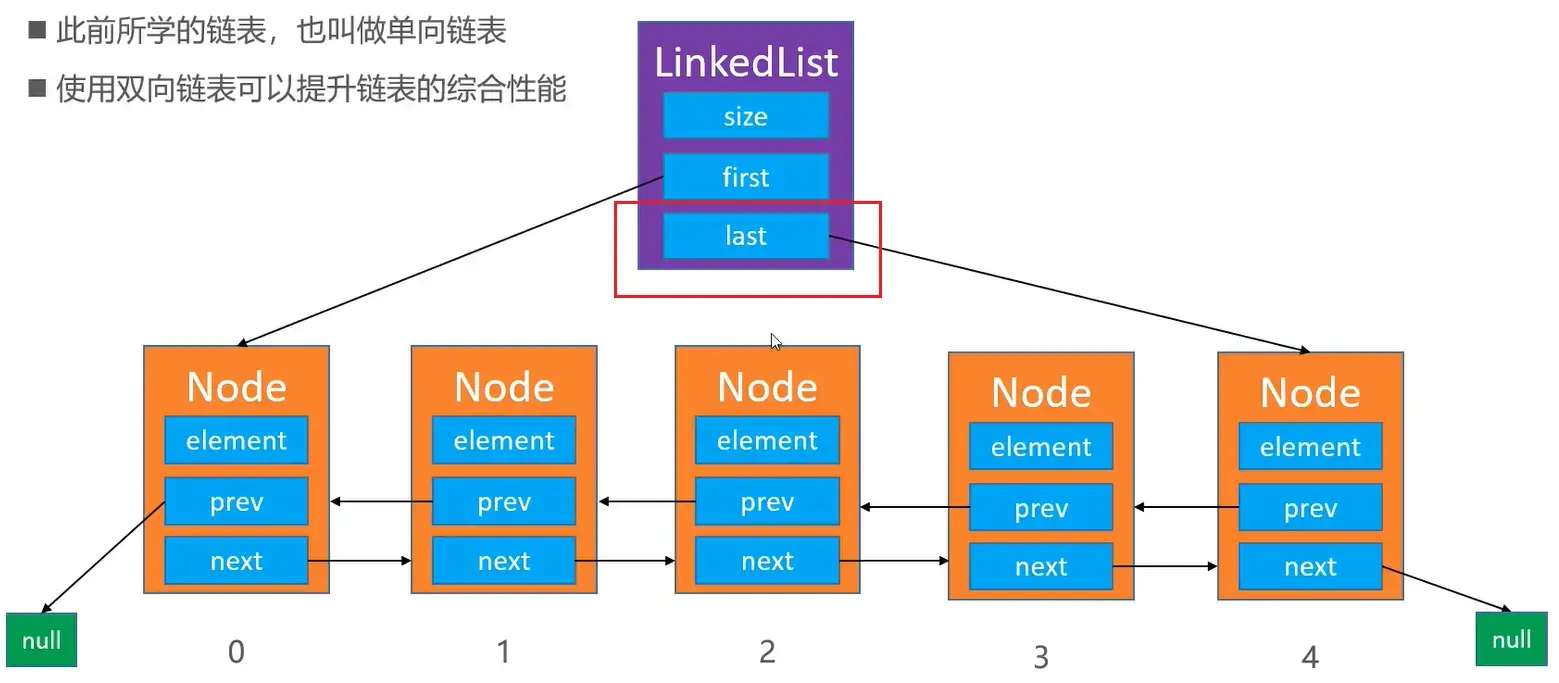
# 双向链表
# 概述
多了个 last 指针，指向尾结点
代码实现：
public class LinkedList<E> extends AbstractList<E> {
private Node<E> first;
private Node<E> last;
private static class Node<E> {
E element;
Node<E> prev;
Node<E> next;
public Node(Node<E> prev, E element, Node<E> next) {
this.prev = prev;
this.element = element;
this.next = next;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
if (prev != null) {
sb.append(prev.element);
} else {
sb.append("null");
}
sb.append("_").append(element).append("_");
if (next != null) {
sb.append(next.element);
} else {
sb.append("null");
}
return sb.toString();
}
}
@Override
public void clear() {
size = 0;
first = null;
last = null;
}
@Override
public E get(int index) {
return node(index).element;
}
@Override
public E set(int index, E element) {
/**
* 最好：O(1)
* 最坏：O(n)
* 平均：O(n)
*/
Node<E> node = node(index);
E old = node.element;
node.element = element;
return old;
}
@Override
public void add(int index, E element) {
/**
* 最好：O(1)
* 最坏：O(n)
* 平均：O(n)
*/
rangeCheckForAdd(index);
// size == 0
// index == 0
if (index == size) { // 3、往最后面添加元素
Node<E> oldLast = last;
last = new Node<>(oldLast, element, null);
if (oldLast == null) { // 4、这是链表添加的第一个元素
first = last;
} else {
oldLast.next = last;
}
} else {
Node<E> next = node(index); // 1、正常中间添加的情况
Node<E> prev = next.prev;
Node<E> node = new Node<>(prev, element, next);
next.prev = node;
if (prev == null) { // 2、最前面添加元素的情况 -- index == 0
first = node;
} else {
prev.next = node;
}
}
size++;
}
@Override
public E remove(int index) {
rangeCheck(index);
// 共三种情况：前、中、后
Node<E> node = node(index);
Node<E> prev = node.prev;
Node<E> next = node.next;
if (prev == null) { // index == 0
first = next;
} else {
prev.next = next;
}
if (next == null) { // index == size - 1
last = prev;
} else {
next.prev = prev;
}
size--;
return node.element;
}
@Override
public int indexOf(E element) {
if (element == null) {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (node.element == null) return i;
node = node.next;
}
} else {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (element.equals(node.element)) return i;
node = node.next;
}
}
return ELEMENT_NOT_FOUND;
}
/**
* 获取index位置对应的节点对象
* @param index
* @return
*/
private Node<E> node(int index) {
rangeCheck(index);
if (index < (size >> 1)) {
Node<E> node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
} else {
Node<E> node = last;
for (int i = size - 1; i > index; i--) {
node = node.prev;
}
return node;
}
}
@Override
public String toString() {
StringBuilder string = new StringBuilder();
string.append("size=").append(size).append(", [");
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (i != 0) {
string.append(", ");
}
string.append(node); // 打印节点
node = node.next;
}
string.append("]");
return string.toString();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
# 注意事项
为了更好的验证接口的测试结果，可以在 Node<E> 里面重写一个 toSting() 方法来打印节点，定义节点字符串拼接格式。
其中：
- 一个
toString是LinkedList<E>的 - 一个
toString是Node<E>的
# 总结
# 双向链表 vs 单向链表
对比 remove 操作：
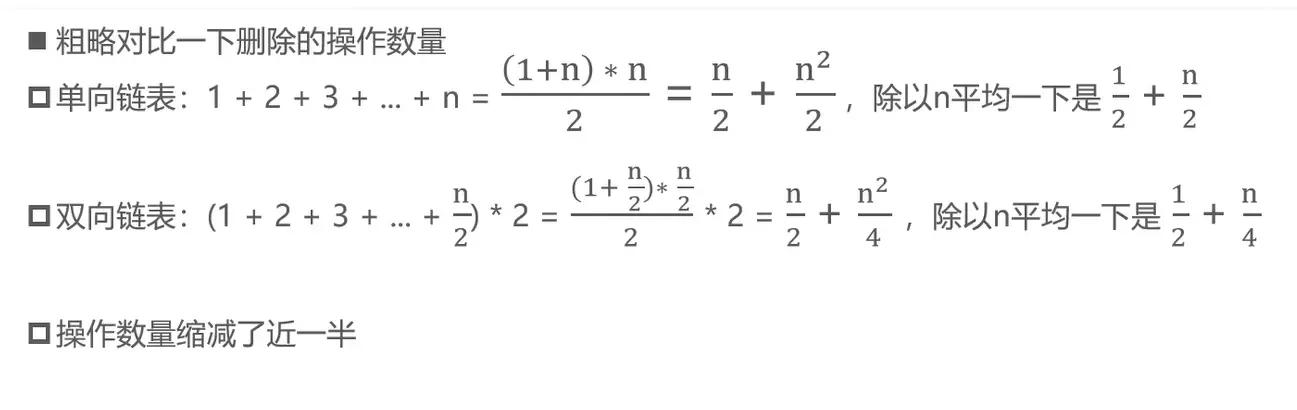
# 双向链表 vs 动态数组
主要是时间与空间上的对比：
# 有了双向链表，单向链表是否就没有任何用处了？
并非如此，在 哈希表的设计 中就用到了单链表。
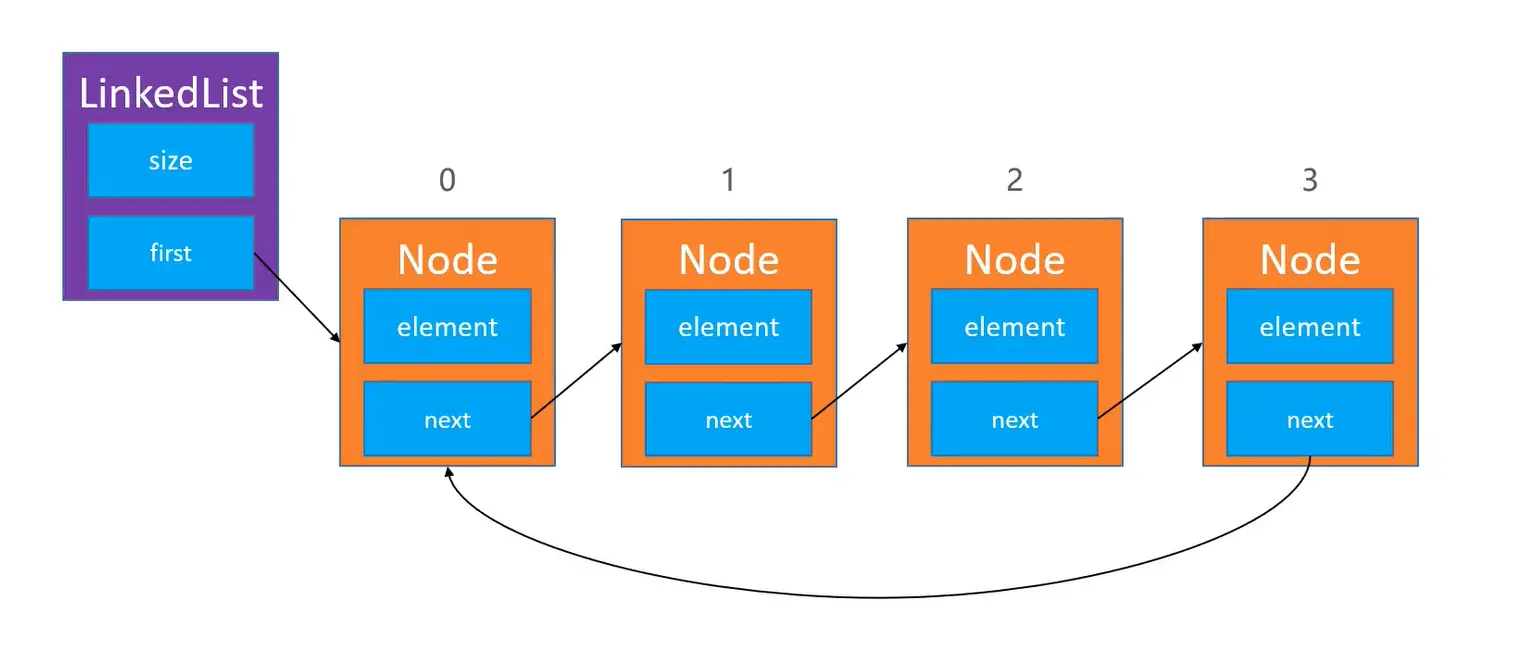
# 单向循环链表
具体如下图所示：
代码实现：
public class SingleCircleLinkedList<E> extends AbstractList<E> {
private Node<E> first;
private static class Node<E> {
E element;
Node<E> next;
public Node(E element, Node<E> next) {
this.element = element;
this.next = next;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append(element).append("_").append(next.element);
return sb.toString();
}
}
@Override
public void clear() {
size = 0;
first = null;
}
@Override
public E get(int index) {
return node(index).element;
}
@Override
public E set(int index, E element) {
Node<E> node = node(index);
E old = node.element;
node.element = element;
return old;
}
@Override
public void add(int index, E element) {
rangeCheckForAdd(index);
if (index == 0) {
// 不能改变原来的first
Node<E> newFirst = new Node<>(element, first);
// 拿到最后一个节点
Node<E> last = (size == 0) ? newFirst : node(size - 1);
last.next = newFirst;
first = newFirst;
} else {
Node<E> prev = node(index - 1);
prev.next = new Node<>(element, prev.next);
}
size++;
}
@Override
public E remove(int index) {
rangeCheck(index);
Node<E> node = first;
if (index == 0) {
if (size == 1) {
// 链表只有一个元素的时候
first = null;
} else {
// 删除第一个元素的时候
Node<E> last = node(size - 1);
first = first.next;
last.next = first;
}
} else {
// 正常删除
Node<E> prev = node(index - 1);
node = prev.next;
prev.next = node.next;
}
size--;
return node.element;
}
@Override
public int indexOf(E element) {
if (element == null) {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (node.element == null) return i;
node = node.next;
}
} else {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (element.equals(node.element)) return i;
node = node.next;
}
}
return ELEMENT_NOT_FOUND;
}
/**
* 获取index位置对应的节点对象
* @param index
* @return
*/
private Node<E> node(int index) {
rangeCheck(index);
Node<E> node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
}
@Override
public String toString() {
StringBuilder string = new StringBuilder();
string.append("size=").append(size).append(", [");
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (i != 0) {
string.append(", ");
}
string.append(node);
node = node.next;
}
string.append("]");
return string.toString();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
# 双向循环链表
代码实现：
利用 current 可解决约瑟夫问题
public class CircleLinkedList<E> extends AbstractList<E> {
private Node<E> first;
private Node<E> last;
private Node<E> current;
private static class Node<E> {
E element;
Node<E> prev;
Node<E> next;
public Node(Node<E> prev, E element, Node<E> next) {
this.prev = prev;
this.element = element;
this.next = next;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
if (prev != null) {
sb.append(prev.element);
} else {
sb.append("null");
}
sb.append("_").append(element).append("_");
if (next != null) {
sb.append(next.element);
} else {
sb.append("null");
}
return sb.toString();
}
}
public void reset() {
current = first;
}
public E next() {
if (current == null) return null;
current = current.next;
return current.element;
}
public E remove() {
if (current == null) return null;
Node<E> next = current.next;
E element = remove(current);
if (size == 0) {
current = null;
} else {
current = next;
}
return element;
}
@Override
public void clear() {
size = 0;
first = null;
last = null;
}
@Override
public E get(int index) {
return node(index).element;
}
@Override
public E set(int index, E element) {
Node<E> node = node(index);
E old = node.element;
node.element = element;
return old;
}
@Override
public void add(int index, E element) {
rangeCheckForAdd(index);
// size == 0
// index == 0
if (index == size) { // 往最后面添加元素
Node<E> oldLast = last;
last = new Node<>(oldLast, element, first);
if (oldLast == null) { // 这是链表添加的第一个元素
first = last;
first.next = first;
first.prev = first;
} else {
oldLast.next = last;
first.prev = last;
}
} else { // 其他位置添加元素
Node<E> next = node(index);
Node<E> prev = next.prev;
Node<E> node = new Node<>(prev, element, next);
next.prev = node;
prev.next = node;
if (next == first) { // index == 0，添加头节点的时候
first = node;
}
}
size++;
}
@Override
public E remove(int index) {
rangeCheck(index);
return remove(node(index));
}
private E remove(Node<E> node) {
if (size == 1) { // 只有一个元素的情况
first = null;
last = null;
} else { // 其他位置
Node<E> prev = node.prev;
Node<E> next = node.next;
prev.next = next;
next.prev = prev;
if (node == first) { // index == 0，删除头节点
first = next;
}
if (node == last) { // index == size - 1，删除尾结点
last = prev;
}
}
size--;
return node.element;
}
@Override
public int indexOf(E element) {
if (element == null) {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (node.element == null) return i;
node = node.next;
}
} else {
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (element.equals(node.element)) return i;
node = node.next;
}
}
return ELEMENT_NOT_FOUND;
}
/**
* 获取index位置对应的节点对象
* @param index
* @return
*/
private Node<E> node(int index) {
rangeCheck(index);
if (index < (size >> 1)) {
Node<E> node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
} else {
Node<E> node = last;
for (int i = size - 1; i > index; i--) {
node = node.prev;
}
return node;
}
}
@Override
public String toString() {
StringBuilder string = new StringBuilder();
string.append("size=").append(size).append(", [");
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (i != 0) {
string.append(", ");
}
string.append(node);
node = node.next;
}
string.append("]");
return string.toString();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
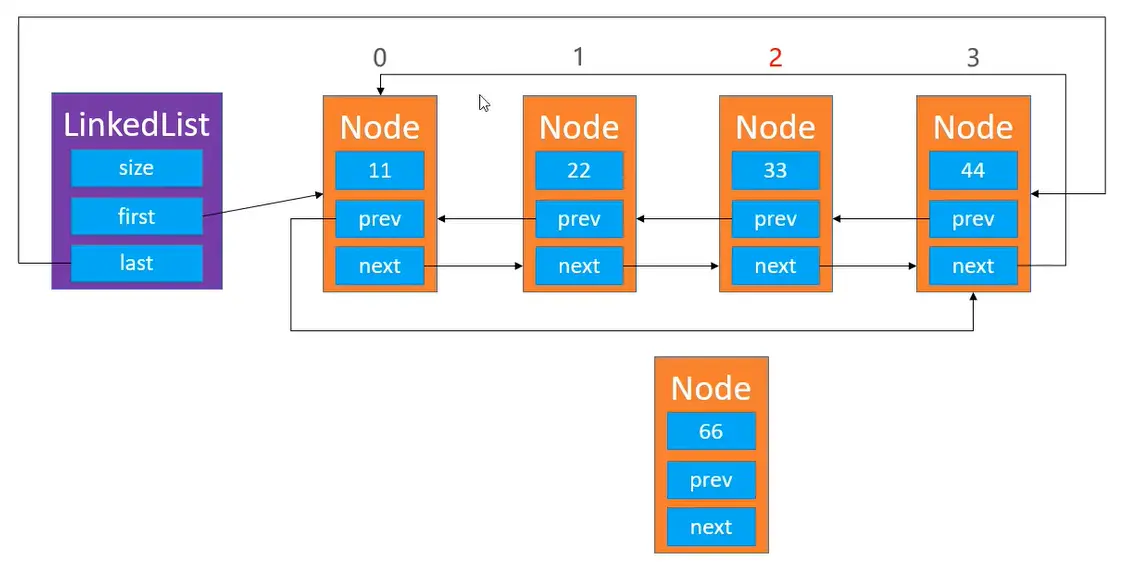
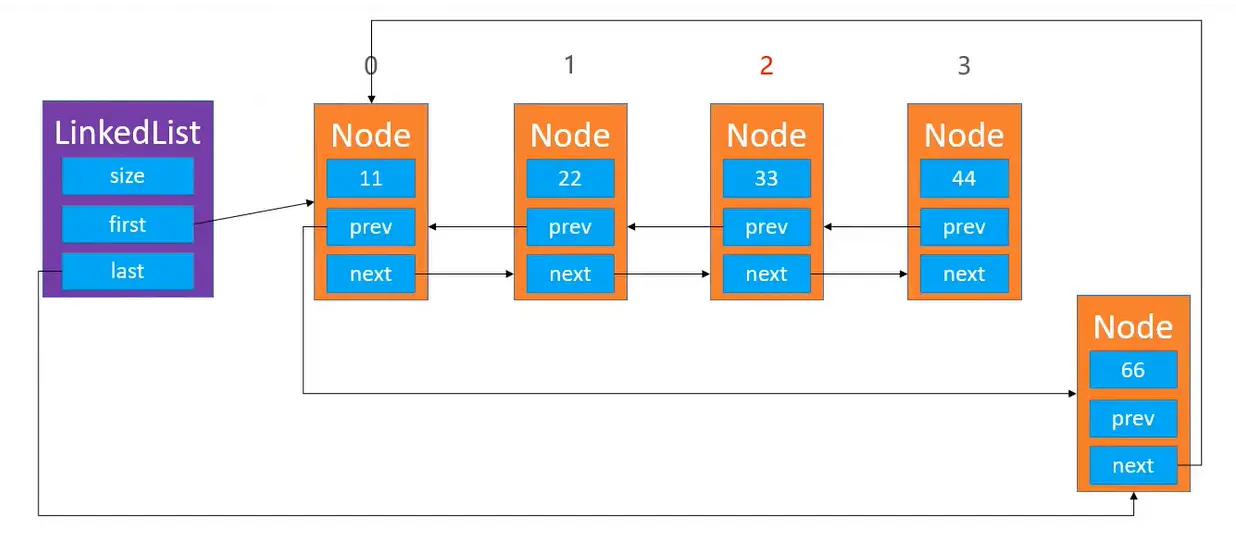
注意：添加和删除操作的判断条件
具体如图所示：
添加前
添加后
# 静态链表
前面所学习的链表，是依赖于指针（引用）实现的。 -- 比如说：first、prev 那些指针
但有些编程语言是没有指针的，比如 basic、fortran 语言
没有指针，通过数组来模拟链表，称为静态链表。
上次更新: 2024/9/25 11:16:13