Tire

需求分析

如何判断一堆不重复的字符串是否以某个前缀开头？

• 用 Set\Map 存储字符串（不重复）
• 遍历所有字符串进行判断
• 缺点：时间复杂度 O(n)

有没有更优的数据结构实现前缀搜索？

Tire（和 Tree 同音）

简介

• Trie 也叫做字典树、前缀树 (Prefix Tree)、单词查找树。
• Trie 搜索字符串的效率主要跟字符串的长度有关。

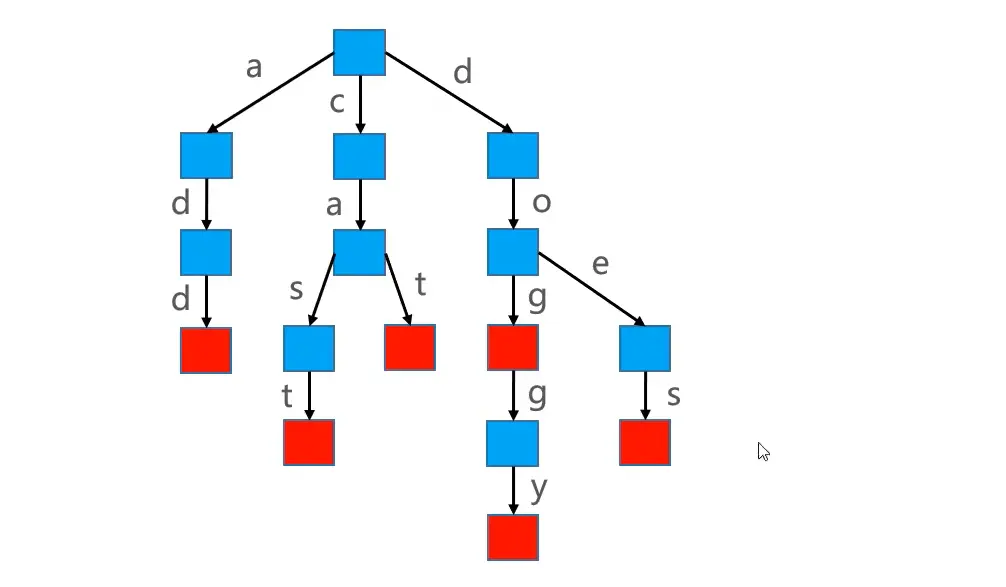
假设使用 Trie 存储 cat、dog、doggy、does、cast、add 六个单词，结果如下所示

接口设计

有两种设计方案：

1. 第一种仅仅是存储字符串。（像 set 集合）
2. 第二种是存储字符串的同时可以再存储一个 value（像 map 接口）

分析：

第二种设计方案更为通用，比如说我们要做一个通讯录，以某个人的姓名作为 key，然后以他的详细信息作为 value（其他电话号码、邮箱、生日等各种详细信息）

public interface Trie <V> {
	int size(); 
	boolean isEmpty(); 
	void clear(); 
	boolean contains(String str); 
	V add(String str, V value); 
	V remove(String str); 
	boolean starswith(String prefix);
}

Node 设计

孩子节点集合解析（HashMap<Character, Node<V>> children;）：

• key 相当于代表的是路径值，Character 字符类型可以是英文也可以是中文
• value 是嵌套了当前节点下的所有子节点，方便后面节点值寻找
• word：true 为已存储单词（红色），false 为非单词（蓝色）

    /**
     * Trie 中的节点类，包含父节点、孩子节点集合、字符、值以及表示是否为一个完整单词的标志。
     *
     * @param <V> 值的类型
     */
    private static class Node<V> {
        Node<V> parent; // 父节点
        HashMap<Character, Node<V>> children; // 孩子节点集合
        Character character; // 字符，为删除做准备
        V value; // 节点对应的值，也就是整个单词
        boolean word; // 是否为单词的结尾（是否为一个完整的单词）

        /**
         * 构造函数，初始化节点时需要指定父节点。(在添加节点时用到）
         *
         * @param parent 父节点
         */
        public Node(Node<V> parent) {
            this.parent = parent;
        }
    }

完整代码实现

/**
 * Trie（字典树）数据结构，用于存储字符串集合，支持添加、查询、删除等操作。
 *
 * @param <V> 值的类型
 */
public class Trie<V> {

    /** Trie 中存储的单词数量 */
    private int size;

    /** 根节点 */
    private Node<V> root;

    /**
     * Trie 中的节点类，包含父节点、孩子节点集合、字符、值以及表示是否为一个完整单词的标志。
     *
     * @param <V> 值的类型
     */
    private static class Node<V> {
        Node<V> parent; // 父节点
        HashMap<Character, Node<V>> children; // 孩子节点集合
        Character character; // 字符，为删除做准备
        V value; // 节点对应的值，也就是整个单词
        boolean word; // 是否为单词的结尾（是否为一个完整的单词）

        /**
         * 构造函数，初始化节点时需要指定父节点。(在添加节点时用到）
         *
         * @param parent 父节点
         */
        public Node(Node<V> parent) {
            this.parent = parent;
        }
    }

    /**
     * 获取 Trie 中存储的单词数量。
     *
     * @return Trie 中存储的单词数量
     */
    public int size() {
        return size;
    }

    /**
     * 判断 Trie 是否为空。
     *
     * @return 如果 Trie 为空，则返回 true；否则返回 false
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 清空 Trie，将单词数量重置为 0。
     */
    public void clear() {
        size = 0;
        root = null;
    }

    /**
     * 根据指定的键获取对应的值。
     *
     * @param key 键
     * @return 如果键存在且是一个完整的单词，则返回对应的值；否则返回 null
     */
    public V get(String key) {
        Node<V> node = node(key);
        return (node != null && node.word) ? node.value : null;
    }

    /**
     * 判断 Trie 是否包含指定的键。
     *
     * @param key 键
     * @return 如果 Trie 包含指定的键且是一个完整的单词，则返回 true；否则返回 false
     */
    public boolean contains(String key) {
        Node<V> node = node(key);
        return node != null && node.word;
    }

    /**
     * 添加键值对到 Trie 中。如果键已经存在，则更新对应的值；否则新增一个单词。
     *
     * @param key   键
     * @param value 值
     * @return 如果添加的键已经存在，则返回对应的旧值；否则返回 null
     */
    public V add(String key, V value) {
        keyCheck(key);

        // 创建根节点
        if (root == null) {
            root = new Node<>(null);
        }

        // 获取 Trie 根节点
        Node<V> node = root;
        // 获取键的长度
        int len = key.length();
        // 遍历键的每个字符
        for (int i = 0; i < len; i++) {
            // 获取当前字符
            char c = key.charAt(i);
            // 判断当前节点的孩子节点集合是否为空
            boolean emptyChildren = (node.children == null);
            // 获取当前字符对应的孩子节点
            Node<V> childNode = emptyChildren ? null : node.children.get(c);
            // 如果当前字符对应的孩子节点为空，说明该字符在当前节点的孩子节点集合中不存在
            if (childNode == null) {
                // 创建新的孩子节点，并将其加入到当前节点的孩子节点集合中
                childNode = new Node<>(node);
                childNode.character = c;
                // 判断孩子节点集合是否为空的同时，避免了每次都要创建新的 HashMap 对象，提高了效率
                node.children = emptyChildren ? new HashMap<>(16) : node.children;
                node.children.put(c, childNode);
            }
            // 将当前节点移动到其对应的孩子节点上，继续下一层的遍历
            node = childNode;
        }

        // 1 - 已经存在这个单词, 覆盖, 返回旧值
        if (node.word) {
            V oldValue = node.value;
            node.value = value;
            return oldValue;
        }

        // 2 - 不存在这个单词, 新增这个单词
        node.word = true;
        node.value = value;
        size++;
        return null;
    }

    /**
     * 移除 Trie 中的指定键。如果键存在且是一个完整的单词，将其从 Trie 中移除。
     *
     * @param key 键
     * @return 如果键存在且是一个完整的单词，则返回对应的值；否则返回 null
     */
    public V remove(String key) {
        Node<V> node = node(key);
        
        // 如果不是单词结尾，不用作任何处理
        if (node == null || !node.word) {
            return null;
        }
        size--;
        V oldValue = node.value;

        // 如果还有子节点
        if (node.children != null && !node.children.isEmpty()) {
            node.word = false;
            node.value = null;
            return oldValue;
        }

        // 没有子节点
        Node<V> parent = null;
        while ((parent = node.parent) != null) {
            parent.children.remove(node.character);
            if (parent.word || !parent.children.isEmpty()) {
                break;
            }
            node = parent;
        }
        return oldValue;
    }

    /**
     * 判断 Trie 是否包含指定前缀。
     *
     * @param prefix 前缀
     * @return 如果 Trie 包含指定前缀，则返回 true；否则返回 false
     */
    public boolean startsWith(String prefix) {
        return node(prefix) != null;
    }

    /**
     * 根据传入字符串，找到最后一个节点。
     * 例如输入 dog
     * 找到 g
     *
     * @param key 键
     * @return 如果键存在，则返回对应的节点；否则返回 null
     */
    private Node<V> node(String key) {
        keyCheck(key);

        Node<V> node = root;
        int len = key.length();
        for (int i = 0; i < len; i++) {
            if (node == null || node.children == null || node.children.isEmpty()) {
                return null;
            }
            char c = key.charAt(i);
            node = node.children.get(c);
        }
        return node;
    }

    /**
     * 检查键是否合法，不允许为空。
     *
     * @param key 键
     */
    private void keyCheck(String key) {
        if (key == null || key.length() == 0) {
            throw new IllegalArgumentException("key must not be empty");
        }
    }
}

总结

1. Trie 的优点：搜索前缀的效率主要跟前缀的长度有关

2. Trie 的缺点：需要耗费大量的内存（一个字符一个节点），因此还有待改进

3. 更多 Trie 相关的数据结构和算法

   • Double-array Trie、Suffix Tree（后缀树）、Patricia Tree、Crit-bit Tree、AC 自动机