困难篇

4. 寻找两个正序数组的中位数 (opens new window)

何为分治？

分治（Divide and Conquer）是一种算法设计策略，它将问题划分为更小的子问题，然后解决子问题并将它们的结果合并以获得原始问题的解。分治算法通常包括三个步骤：分解（Divide）、解决（Conquer）和合并（Combine）。在分治算法中，问题被逐步划分成更小的子问题，然后对子问题进行递归求解，最后将子问题的解合并起来得到原始问题的解。

何为二分查找？

二分查找是一种在有序数组中查找特定元素的算法。它通过将目标值与数组的中间元素进行比较，然后根据比较结果缩小查找范围，逐步逼近目标值。如果中间元素等于目标值，则查找成功；如果中间元素大于目标值，则在数组的左半部分继续查找；如果中间元素小于目标值，则在数组的右半部分继续查找。通过不断缩小查找范围，最终可以找到目标值或确定目标值不存在于数组中。

题解

/**
 * 寻找两个正序数组的中位数 -- 数组, 二分查找, 分治
 *
 * @author 沉梦听雨
 **/
@SuppressWarnings("all")
public class _4_寻找两个正序数组的中位数 {

    // 算法的时间复杂度应该为 O(log (m+n))

    /**
     * 1、合并有序数组并找到中位数 -- 2ms(33.34%), 43.8MB(7.71%)
     * <p>
     * 时间复杂度为 O(m + n)，空间复杂度为 O(m + n)
     */
    class Solution1 {
        public double findMedianSortedArrays(int[] nums1, int[] nums2) {
            int len1 = nums1.length;
            int len2 = nums2.length;
            int[] nums = new int[len1 + len2];
            int i = 0;
            int j = 0;
            int k = 0;
            while (i < len1 && j < len2) {
                if (nums1[i] < nums2[j]) {
                    nums[k] = nums1[i];
                    i++;
                } else {
                    nums[k] = nums2[j];
                    j++;
                }
                k++;
            }
            while (i < len1) {
                nums[k] = nums1[i];
                i++;
                k++;
            }
            while (j < len2) {
                nums[k] = nums2[j];
                j++;
                k++;
            }
            if (nums.length % 2 != 0) {
                return (double) nums[nums.length / 2];
            } else {
                int pre = nums[nums.length / 2 - 1];
                int mid = nums[nums.length / 2];
                return (pre + mid) / 2.0;
            }
        }
    }

    /**
     * 2、分治 -- 1ms(100%), 43.8MB(9.44%)
     * <p>
     * 时间复杂度为 O( log(m + n) ), 空间复杂度为 O( log(m + n) )
     */
    class Solution2 {
        private int m;
        private int n;
        private int[] nums1;
        private int[] nums2;

        public double findMedianSortedArrays(int[] nums1, int[] nums2) {
            m = nums1.length;
            n = nums2.length;
            this.nums1 = nums1;
            this.nums2 = nums2;
            int a = f(0, 0, (m + n + 1) / 2); // 找到中位数左边的元素
            int b = f(0, 0, (m + n + 2) / 2); // 找到中位数右边的元素
            return (a + b) / 2.0; // 返回中位数
        }

        private int f(int i, int j, int k) {
            if (i >= m) {
                return nums2[j + k - 1]; // nums1 数组已经遍历完，返回 nums2 数组中对应位置的元素
            }
            if (j >= n) {
                return nums1[i + k - 1]; // nums2 数组已经遍历完，返回 nums1 数组中对应位置的元素
            }
            if (k == 1) {
                return Math.min(nums1[i], nums2[j]); // 达到中位数位置，返回两个数组当前位置上较小的元素
            }
            int p = k / 2; // 将 k 分成两部分
            int x = i + p - 1 < m ? nums1[i + p - 1] : 1 << 30; // 获取 nums1 数组中第 p 个元素，如果超出数组范围，设置为一个较大的值
            int y = j + p - 1 < n ? nums2[j + p - 1] : 1 << 30; // 获取 nums2 数组中第 p 个元素，如果超出数组范围，设置为一个较大的值
            return x < y ? f(i + p, j, k - p) : f(i, j + p, k - p); // 如果 x 小于 y，则在 nums1 数组的右侧或者 nums2 数组的左侧继续查找，否则在 nums2 数组的右侧或者 nums1 数组的左侧继续查找
        }
    }
}

10. 正则表达式匹配

主要思路是使用动态规划方法。

思路如下

1. 首先，定义一个二维布尔数组 dp，其中 dp[i][j] 表示 s 的前 i 个字符是否与 p 的前 j 个字符匹配。
2. 然后，初始化 dp 数组，根据 p 的偶数位置是否为 * 来确定 dp[0][j] 的值。
3. 接下来，遍历 s 和 p，根据 p 的当前字符是否为 * 来更新 dp 数组的值。
4. 最后，返回 dp[m][n]，即 s 和 p 是否匹配。

具体实现过程如下

1. 定义一个二维布尔数组 dp，用于存储 s 和 p 的匹配情况。
2. 初始化 dp 数组的第一列，根据 p 的偶数位置是否为 * 来确定 dp[0][j] 的值。
3. 遍历 s 和 p，根据 p 的当前字符是否为 * 来更新 dp 数组的值。
   • 如果 p 的当前字符是 *，则 dp[i][j] 的值可以由 dp[i][j-2]（不使用 *）或 dp[i-1][j]（使用 *）转移而来。
   • 否则，dp[i][j] 的值可以由 dp[i-1][j-1]（当前字符匹配）或 dp[i-1][j-1]（当前字符不匹配但 p 的当前字符为 .）转移而来。
4. 返回 dp[m][n]，即 s 和 p 是否匹配。

代码如下

    /**
     * 1、动态规划 -- 1ms(100%), 39.79MB(85.76%)
     * <p>
     * 时间复杂度为 O(m * n)，空间复杂度为 O(m * n)
     */
    class Solution {
        public boolean isMatch(String s, String p) {
            int m = s.length();
            int n = p.length();

            // 初始化dp数组，dp[i][j]表示s的前i个字符是否与p的前j个字符匹配
            boolean[][] dp = new boolean[m + 1][n + 1];
            // 初始化 dp[o][o]= true 表示空字符串和空正则表达式是匹配的。
            dp[0][0] = true;

            // 初始化第一行，如果p的偶数位置是*，则dp[0][j] = dp[0][j - 2]
            for (int j = 2; j <= n; j += 2) {
                dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
            }

            // 遍历s和p，动态规划
            for (int i = 1; i <= m; i++) {
                for (int j = 1; j <= n; j++) {
                    // 如果p的当前字符是*，则dp[i][j] = dp[i][j - 2] || (dp[i - 1][j] && (s[i - 1] == p[j - 2] || p[j - 2] == '.'))
                    if (p.charAt(j - 1) == '*') {
                        // 考虑了 * 匹配 0 次和匹配至少 1 次的情况
                        dp[i][j] = dp[i][j - 2] || (dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.'));
                    } else {
                        // 否则，dp[i][j] = dp[i - 1][j - 1] && (s[i - 1] == p[j - 1] || p[j - 1] == '.')
                        // 处理普通字符匹配的情况，确保了当前位置的匹配状态
                        dp[i][j] = dp[i - 1][j - 1] && (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.');
                    }
                }
            }

            // 返回dp[m][n]
            return dp[m][n];
        }
    }

问题

初始化第一列，如果 p 的偶数位置是 ，则 dp[0][j] = dp[0][j - 2]。为什么？

这是因为正则表达式中的 * 表示前面的字符可以重复零次或多次。

所以，当 * 出现在偶数位置时，它前面的字符可以被忽略，即重复零次。

让我们以一个例子来说明：

• 假设正则表达式 p 为 a*b*cd，而目标字符串 s 为 acd。
• 在这个例子中，a* 中的 a 可以重复零次，即可以没有 a。同样，b* 中的 b 也可以重复零次，即可以没有 b。因此，正则表达式可以匹配目标字符串。
• 对应到动态规划数组中，dp[0][j] 表示【空字符串】是否能够匹配 p 的前 j 个字符。
• 如果 p[j-1] 是 *（偶数位置），则 * 可以表示零次，所以 dp[0][j] 的值可以参考 dp[0][j-2]，即忽略 * 及其前面的字符。
• 这样的初始化保证了在动态规划的过程中，即使出现 *，也会考虑到它可以重复零次的情况，从而正确地判断正则表达式是否匹配目标字符串。

动态规划

使用两个嵌套的循环遍历 s 和 p，根据字符匹配规则更新动态规划数组。

1. 对于 * 的情况，根据前面的状态进行更新；
   • dp[i][j - 2]：表示忽略掉 p 的 * 和前面的字符，相当于 * 匹配了 0 次。例如，对于 s = "abc"，p = "ab*c"，这里的 * 匹配了 0 次。
   • dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.')：表示 * 匹配了至少 1 次，且 s 的当前字符与 * 前面的字符相同，或者 * 前面的字符是 .（可以匹配任意字符）。
   • 例如，对于 s = "aa"，p = "a*"，这里的 * 匹配了 2 次。
2. 对于其他字符的情况，则根据单字符匹配规则更新。
   • dp[i - 1][j - 1]：表示 s 的前 i - 1 个字符和 p 的前 j - 1 个字符已经匹配，此时判断当前字符是否匹配。
   • (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.')：表示当前字符匹配的条件，即 s 的第 i - 1 个字符与 p 的第 j - 1 个字符相同，或者 p 的第 j - 1 个字符是 .（可以匹配任意字符）。
   • 否则，dp[i][j] = false。

23. 合并 K 个升序链表 (opens new window)

题目描述

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] 按 升序 排列
• lists[i].length 的总和不超过 10^4

方法一：优先队列（小根堆）

    /**
     * 1、优先队列（小根堆） -- 4ms(70.11%), 43.41MB(10.57%)
     * <p>
     * 时间复杂度：O(nlogk)，其中 n 是所有链表节点数目的总和，而 k 是题目给定的链表数目。
     * <p>
     * 空间复杂度：O(k)
     */
    class Solution {
        public ListNode mergeKLists(ListNode[] lists) {
            // 创建一个优先队列 queue，元素为 ListNode，并根据 ListNode 的 val 属性进行排序
            PriorityQueue<ListNode> queue = new PriorityQueue<>((a, b) -> a.val - b.val);

            // 遍历 lists 数组，将每个链表的头节点加入优先队列中
            for (ListNode head : lists) {
                // 如果当前链表的头节点不为空
                if (head != null) {
                    // 将【当前链表的头节点】加入优先队列中，注意：是当前链表的头结点
                    queue.offer(head);
                }
            }

            // 创建一个虚拟的头节点 dummy
            ListNode dummy = new ListNode();
            // 创建一个指针 cur，初始时指向虚拟头节点 dummy
            ListNode cur = dummy;
            // 当优先队列 queue 不为空时
            while (!queue.isEmpty()) {
                // 从优先队列 queue 中取出一个节点 node
                ListNode node = queue.poll();
                // 如果当前节点的下一个节点不为空
                if (node.next != null) {
                    // 将当前节点的下一个节点加入优先队列中
                    queue.offer(node.next);
                }
                // 将当前节点 node 加入到 cur 的下一个节点
                cur.next = node;
                // 将 cur 指针移动到下一个节点
                cur = cur.next;
            }

            // 返回虚拟头节点的下一个节点，即合并后的链表的头节点
            return dummy.next;
        }
    }

25. K 个一组翻转链表 (opens new window)

题目描述

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

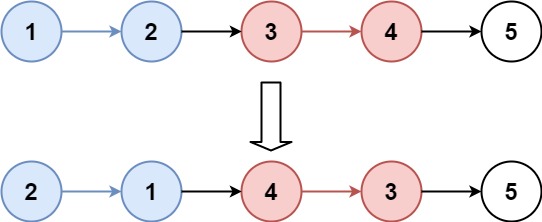
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

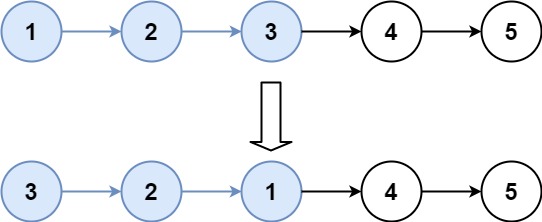
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

• 链表中的节点数目为 n
• 1 <= k <= n <= 5000
• 0 <= Node.val <= 1000

**进阶：**你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

方法一：虚拟头节点 + 双指针

    /**
     * 1、虚拟头节点 + 双指针 -- 0ms(100.00%), 43.05MB(14.82%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public ListNode reverseKGroup(ListNode head, int k) {
            // 创建虚拟头节点
            ListNode dummy = new ListNode(0, head);
            // 初始化两个指针 pre 和 cur，均指向虚拟头节点
            ListNode pre = dummy, cur = dummy;
            // 循环遍历链表
            while (cur.next != null) {
                // 将 cur 指针移动 k 次
                for (int i = 0; i < k; i++) {
                    cur = cur.next;
                    // 如果 cur 为 null，说明剩余节点不足 k 个，直接返回虚拟头节点的下一个节点
                    if (cur == null) {
                        return dummy.next;
                    }
                }
                // 记录当前 cur 指针的下一个节点
                ListNode tmp = cur.next;
                // 将 cur 指针的 next 置为 null，断开当前 k 个节点的链表
                cur.next = null;
                // 获取当前 k 个节点的起始节点
                ListNode start = pre.next;
                // 将 pre 节点的 next 指向反转后的链表
                pre.next = reverseList(start);
                // 将反转后的链表的尾节点的 next 指向 tmp，重新连接链表
                start.next = tmp;
                // 更新 pre 和 cur 指针位置
                pre = start;
                cur = pre;
            }
            // 返回虚拟头节点的下一个节点，即整个链表的头节点
            return dummy.next;
        }

        /**
         * 反转链表
         *
         * @param head
         * @return
         */
        private ListNode reverseList(ListNode head) {
            // 初始化前驱节点 pre 为 null
            ListNode pre = null;
            // 当前节点 left 指向链表头节点
            ListNode left = head;
            // 循环遍历链表
            while (left != null) {
                // 临时节点 right 保存当前节点的下一个节点
                ListNode right = left.next;
                // 将当前节点的 next 指针反转，指向前驱节点 pre
                left.next = pre;
                // 将前驱节点 pre 更新为当前节点 left
                pre = left;
                // 将当前节点指针 left 移动到下一个节点
                left = right;
            }
            // 返回反转后的链表头节点
            return pre;
        }
    }

41. 缺失的第一个正数 (opens new window)

题目描述

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

输入：nums = [1,2,0]
输出：3

示例 2：

输入：nums = [3,4,-1,1]
输出：2

示例 3：

输入：nums = [7,8,9,11,12]
输出：1

提示：

• 1 <= nums.length <= 5 * 105
• -231 <= nums[i] <= 231 - 1

方法一：排序 + HashSet

代码

    /**
     * 1、排序 + HashSet -- 20ms(5.5%), 57MB(87.37%)
     * <p>
     * 时间复杂度为：O(nlogn)。
     * <p>
     * 空间复杂度为：O(n)。
     */
    class Solution {
        public int firstMissingPositive(int[] nums) {
            // 创建一个HashSet
            HashSet<Integer> set = new HashSet<>();
            // 对数组进行排序
            Arrays.sort(nums);
            // 获取数组的长度
            int n = nums.length;

            // 将数组中的元素添加到HashSet中
            for (int i = 0; i < n; i++) {
                set.add(nums[i]);
            }
            // 遍历数组，查找第一个不存在的正数
            for (int i = 1; i < nums[n - 1]; i++) {
                // 如果HashSet中不存在该正数，则返回该正数
                if (!set.contains(i)) {
                    return i;
                }
            }

            // 如果数组中的最后一个元素大于0，则返回 该元素加1，否则返回 1
            return nums[n - 1] > 0 ? (nums[n - 1] + 1) : 1;
        }
    }

复杂度分析

1. 时间复杂度：
   • 排序数组的时间复杂度是 O(nlogn)，其中 n 是数组的长度。
   • 遍历数组并将元素添加到 HashSet 的时间复杂度是 O(n)。
   • 第二个循环遍历范围是从 1 到 nums[n - 1]，最坏情况下是 O(n)。
   • 综合考虑，总的时间复杂度是 O(nlogn)。
2. 空间复杂度：
   • HashSet 存储了数组中的所有元素，因此空间复杂度为 O(n)。
   • 除了 HashSet 外，只使用了常数级的额外空间。（符合题目中只使用常数级别额外空间的要求）
   • 综合考虑，总的空间复杂度是 O(n)。

方法二：原地转换

思路分析：

• 不用排序，用交换；

• 缺失的最小正整数一定在 数组长度内 或者 数组长度+1。

    /**
     * 2、原地转换 -- 1ms(5.5%), 53.59MB(98.38%)
     * <p>
     * 时间复杂度为：O(n)。
     * <p>
     * 额外空间复杂度为：O(1)。
     */
    class Solution {
        public int firstMissingPositive(int[] nums) {
            int n = nums.length;

            // 遍历数组
            for (int i = 0; i < n; ++i) {
                // 将当前元素放到正确的位置上，即 nums[i] 应该等于 i + 1
                // 当前元素应该在的位置是 nums[i] - 1，如果不在则进行交换
                // (while)判断条件：当前元素是正整数，当前元素不超过数组的长度，当前元素应该在的位置的元素不等于当前元素
                while (nums[i] >= 1 && nums[i] <= n && nums[i] != nums[nums[i] - 1]) {
                    swap(nums, i, nums[i] - 1);
                }
            }

            // 再次遍历数组，寻找第一个不在正确位置上的元素（缺失的最小正整数一定在数组长度内或者数组长度+1）
            for (int i = 0; i < n; ++i) {
                if (i + 1 != nums[i]) {
                    // 如果找到第一个不在正确位置上的元素，则返回缺失的最小正整数
                    return i + 1;
                }
            }

            // 如果数组中所有元素都在正确位置上，返回数组长度加1
            return n + 1;
        }

        // 交换数组中两个元素的位置
        private void swap(int[] nums, int i, int j) {
            int t = nums[i];
            nums[i] = nums[j];
            nums[j] = t;
        }
    }

42. 接雨水 (opens new window)

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

方法一：双指针

    /**
     * 1、双指针 -- 0ms(100.00%), 43.96MB(5.09%)
     * <p>
     * 时间复杂度为 O(n)
     * <p>
     * 空间复杂度为 O(1)
     */
    class Solution {
        public int trap(int[] height) {
            int res = 0;
            // 定义左指针和右指针
            int left = 0, right = height.length - 1;
            // 初始化左右两边的最大高度
            int leftMax = 0, rightMax = 0;

            // 分别记录左右两边的最大高度
            while (left < right) {
                // 记录当前左边的最大高度
                leftMax = Math.max(leftMax, height[left]);
                // 记录当前右边的最大高度
                rightMax = Math.max(rightMax, height[right]);
                // 比较左右两边的最大高度，并记录
                if (height[left] < height[right]) {
                    res += leftMax - height[left];
                    left++;
                } else {
                    res += rightMax - height[right];
                    right--;
                }
            }

            return res;
        }
    }

代码解析

在这个问题中，为了计算接雨水的数量，我们需要找到每个位置上能够容纳的雨水量。这个雨水量实际上是由当前位置的高度和其左右两侧的最大高度中较小的一个决定的。

在算法的实现中，使用了两个指针 left 和 right，分别指向数组的起始和结束位置。同时，维护两个变量 leftMax 和 rightMax 分别表示左边和右边的最大高度。在每一步迭代中，选择左右两侧中较小的最大高度，然后减去当前位置的高度，得到的差值即为当前位置能够容纳的雨水量。

为什么要选择较小的最大高度呢？这是因为如果我们选择较大的最大高度，那么当前位置可能会被左右两侧较小的高度所限制，导致计算得到的雨水量可能超过实际的容量。因此，为了确保计算的准确性，我们选择较小的最大高度来计算雨水量。

具体的判断逻辑如下：

1. 如果 height[left] < height[right]，则计算并累加雨水量 res += leftMax - height[left]，因为左边的最大高度限制了当前位置的容纳能力。
2. 如果 height[left] >= height[right]，则计算并累加雨水量 res += rightMax - height[right]，因为右边的最大高度限制了当前位置的容纳能力。

这样的选择确保了在移动指针的过程中，我们始终使用较小的最大高度来计算雨水量，从而得到准确的结果。

方法二：动态规划

    /**
     * 2、动态规划 -- 1ms(75.87%), 42.92MB(80.95%)
     * <p>
     * 时间复杂度为 O(n)
     * <p>
     * 空间复杂度为 O(n)
     */
    class Solution {
        public int trap(int[] height) {
            // 获取数组长度
            int n = height.length;
            // 创建两个数组，分别用于存储左侧最大值和右侧最大值
            int[] left = new int[n];
            int[] right = new int[n];
            // 初始化边界值
            left[0] = height[0];
            right[n - 1] = height[n - 1];

            // 遍历数组，计算左侧最大值和右侧最大值
            for (int i = 1; i < n; ++i) {
                // 从左到右
                left[i] = Math.max(left[i - 1], height[i]);
                // 从右到左
                right[n - 1 - i] = Math.max(right[n - i], height[n - 1 - i]);
            }

            // 初始化结果变量
            int res = 0;
            // 遍历数组，计算雨水量
            for (int i = 0; i < n; ++i) {
                res += Math.min(left[i], right[i]) - height[i];
            }
            // 返回雨水量
            return res;
        }
    }

代码解析

这个解法与前面的双指针方法不同，这里通过动态规划来预先计算每个位置左右两侧的最大高度，然后再遍历一次数组计算雨水量。

以下是代码的主要步骤：

1. 创建两个数组 left 和 right，分别用于存储每个位置的左侧最大值和右侧最大值。

2. 初始化 left[0] 为 height[0]，表示数组的第一个元素的左侧最大值即为自身的高度。

3. 初始化 right[n - 1] 为 height[n - 1]，表示数组的最后一个元素的右侧最大值即为自身的高度。

4. 使用一个循环，

   • 从左向右遍历数组，计算每个位置的左侧最大值并存储到数组 left 中。

   • 从右向左遍历数组，计算每个位置的右侧最大值并存储到数组 right 中。

5. 初始化结果变量 res 为零。

6. 再次遍历数组，计算每个位置的雨水量，并累加到 res 中。计算方法为取左右两侧最大值中的较小值减去当前位置的高度。

7. 返回最终的雨水量 res。

这种动态规划的方法通过预先计算左右两侧的最大值，避免了在每个位置都进行比较的过程，从而降低了时间复杂度。这个算法的时间复杂度为 O(n)，空间复杂度为 O(n)。

动态规划的体现

这段代码使用了动态规划的思想来解决接雨水问题。动态规划的关键在于将问题分解为子问题，并使用已解决的子问题的解来构建原问题的解。

具体来说，这里的动态规划包括以下步骤：

1. 左右最大值数组的构建： 首先，通过遍历数组，分别构建两个数组 left 和 right，其中 left[i] 表示元素 height[i] 左侧的最大值，right[i] 表示元素 height[i] 右侧的最大值。
2. 计算雨水量： 一旦得到了左侧和右侧的最大值数组，就可以通过遍历数组，计算每个位置上的雨水量。对于每个位置 i，可以通过取 min(left[i], right[i]) - height[i] 来计算在该位置上可以蓄积的雨水量。
3. 累加雨水量： 将每个位置上计算得到的雨水量进行累加，得到最终的总雨水量。

这里的动态规划思想在于先解决子问题（构建左右最大值数组），然后通过这些子问题的解构建原问题的解（计算雨水量）。这有助于减小问题的复杂度，并使问题更容易理解和解决。

239. 滑动窗口最大值 (opens new window)

题目描述

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

1 <= nums.length <= 105

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

解法思路

1. 使用双端队列： 在维护一个双端队列 deque 时，队列中的元素是按照降序排列的，队首元素即为当前窗口的最大值。
2. 遍历数组： 遍历整个数组，对于每个元素执行以下操作：
   • 在插入新元素前，从队尾移除队列中比新元素小的元素，确保队列中的元素是降序排列的。
   • 将当前元素的索引加入队列的尾部。
   • 移除窗口外的元素，即窗口的大小超过 k。
   • 当窗口的大小达到 k 时，将当前窗口的最大值存入结果数组中。
3. 返回结果： 最终，返回存储最大值的结果数组。

方法一：单调队列

    class Solution {
        public int[] maxSlidingWindow(int[] nums, int k) {
            // 获取数组长度
            int n = nums.length;
            // 存储最终结果的数组
            int[] result = new int[n - k + 1];
            // 双端队列，存储数组元素的索引
            Deque<Integer> deque = new LinkedList<>();

            for (int i = 0; i < nums.length; i++) {
                // 在插入新元素前，移除队列中比新元素小的元素，确保队列中的元素是降序排列的
                while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
                    deque.pollLast();
                }

                // 将当前元素的索引加入队列
                deque.offerLast(i);

                // 移除窗口外的元素，即窗口的大小超过 k
                if (i - deque.peekFirst() >= k) {
                    deque.pollFirst();
                }

                // 计算当前窗口的最大值，存入结果数组中
                if (i + 1 >= k) {
                    result[i + 1 - k] = nums[deque.peekFirst()];
                }
            }

            // 返回结果数组
            return result;
        }
    }

复杂度分析

• 时间复杂度： 每个元素最多被加入和弹出双端队列一次，因此时间复杂度为 O(n)。
• 空间复杂度： 双端队列的空间复杂度为 O(k)，结果数组的空间复杂度为 O(n-k+1)，总体空间复杂度为 O(n)。

双端队列与单调队列的关系

1. 单调队列的定义： 单调队列是指队列中的元素是单调递增或单调递减的。在这个问题中，使用的是单调递减队列。
2. 双端队列的特性： 双端队列可以从队头和队尾同时进行插入和删除操作。这使得双端队列在维护单调性时更加灵活。

因此，可以说所有的单调队列都是双端队列，但并非所有的双端队列都是单调队列。

76. 最小覆盖子串 (opens new window)

题目描述

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

• 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
• 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

示例 2：

输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

示例 3:

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

• m == s.length
• n == t.length
• 1 <= m, n <= 105
• s 和 t 由英文字母组成

**进阶：**你能设计一个在 o(m+n) 时间内解决此问题的算法吗？

解题思路

1. 通过维护左右指针，使得窗口包含目标字符串的全部字符。
2. 在窗口包含全部字符的情况下，不断移动左指针来找到最小的窗口。

方法一：双指针 + 哈希表

    /**
     * 1、滑动窗口解法 -- 双指针 + 哈希表 -- 11ms(75.19%), 42.69MB(78.76%)
     * <p>
     * 时间复杂度为：O(m + 2m) = O(m)，其中 m 是源字符串的长度。
     * <p>
     * 空间复杂度为：O(C)，其中 C 为字符集大小。
     */
    class Solution {
        public String minWindow(String s, String t) {
            int m = s.length();
            int n = t.length();

            // 如果s的长度小于t的长度，则返回空字符串
            if (m < n) {
                return "";
            }

            // 创建一个哈希表来存储目标字符串 t 中每个字符的出现次数
            HashMap<Character, Integer> map = new HashMap<>();
            for (char c : t.toCharArray()) {
                map.put(c, map.getOrDefault(c, 0) + 1);
            }

            // 初始化左右指针、字符计数和最小窗口长度及起始位置
            int left = 0, right = 0, count = n;
            int minLen = Integer.MAX_VALUE;
            int minLeft = 0;

            // 遍历源字符串 s
            while (right < m) {
                char c = s.charAt(right);

                // 如果字符 c 在目标字符串 t 中出现，更新计数和哈希表
                if (map.containsKey(c)) {
                    if (map.get(c) > 0) {
                        count--;
                    }
                    map.put(c, map.get(c) - 1);
                }

                // 如果count等于0，则表示当前窗口包含 t 中的所有字符，移动左指针以找到最小窗口
                while (count == 0) {

                    // 如果当前窗口的长度小于minLen，更新最小窗口的长度和位置
                    if (right - left < minLen) {
                        minLen = right - left;
                        minLeft = left;
                    }

                    // 从左边开始收缩窗口：移动左指针，使窗口变得无效
                    char leftChar = s.charAt(left);
                    if (map.containsKey(leftChar)) {
                        map.put(leftChar, map.get(leftChar) + 1);
                        if (map.get(leftChar) > 0) {
                            count++;
                        }
                    }

                    left++;
                }

                // 移动右指针，扩大窗口
                right++;
            }

            // 如果minLen等于Integer.MAX_VALUE，则表示没有符合条件的窗口，返回空字符串
            // 否则根据最小窗口的位置和长度得到结果子串
            return minLen == Integer.MAX_VALUE ? "" : s.substring(minLeft, minLeft + minLen + 1);
        }
    }

复杂度分析

时间复杂度：

• 遍历源字符串 s，时间复杂度为 O(m)，其中 m 是源字符串的长度。
• 内层循环中，左指针 left 和右指针 right 分别向右移动，但每个字符最多被访问两次（一次为右指针移动，一次为左指针移动），因此内层循环的总操作次数不超过 2m。
• 因此，总体时间复杂度为 O(m + 2m) = O(m)。

空间复杂度：

空间复杂度主要取决于哈希表的空间占用。由于哈希表存储的是目标字符串 t 中每个字符的出现次数，且字符集通常是有限的（常常是英文字母），因此空间复杂度为 O(C)，C 为字符集大小。

总结：

该算法的时间复杂度是线性的，空间复杂度与字符集大小相关。