计算机基础
数据结构与算法
力扣篇
Hot100题解

简单篇

# 简单篇

# 1. 两数之和 (opens new window)

# 题目描述

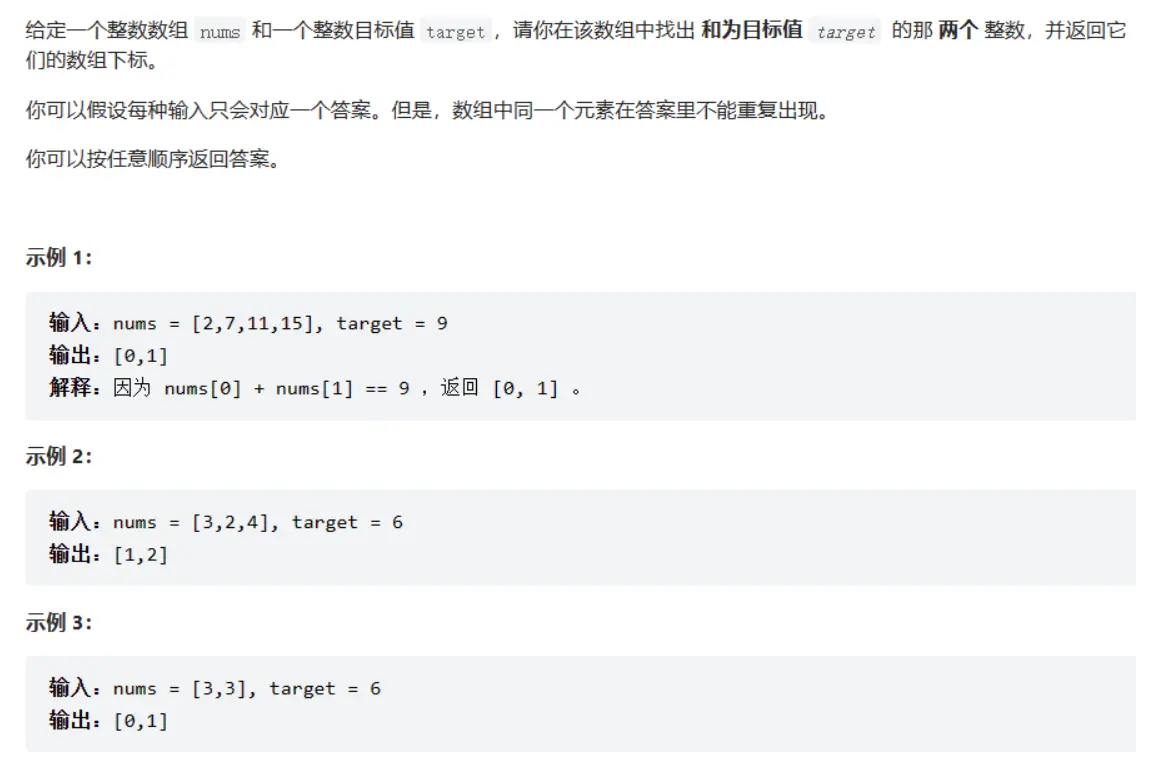
# 方法一：暴力枚举

    /**
     * 1、暴力枚举 -- 49ms(40.58%), 42.8MB(9.48%)
     */
    class Solution {
        public int[] twoSum(int[] nums, int target) {
            int[] result = new int[2];
            for (int i = 0; i < nums.length; i++) {
                for (int j = i + 1; j < nums.length; j++) {
                    if (nums[i] + nums[j] == target) {
                        // return new int[]{i, j};
                        result[0] = i;
                        result[1] = j;
                    }
                }
            }
            return result;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 方法二：哈希表映射

    /**
     * 2、哈希表映射 -- 1ms(99.52%), 42.9MB(5.7%)
     */
   class Solution2 {
        public int[] twoSum(int[] nums, int target) {
            // 创建一个HashMap
            Map<Integer, Integer> map = new HashMap<>();
            // 遍历数组
            for (int i = 0; i < nums.length; i++) {
                // 如果map中包含target - nums[i]，则返回map中target - nums[i]对应的值和i
                if (map.containsKey(target - nums[i])) {
                    return new int[]{map.get(target - nums[i]), i};
                }
                // 将nums[i]和i放入map中
                map.put(nums[i], i);
            }
            // 如果没有找到两个数的和等于target，抛出异常
            throw new IllegalArgumentException("No two sum solution");
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 20. 有效的括号 (opens new window)

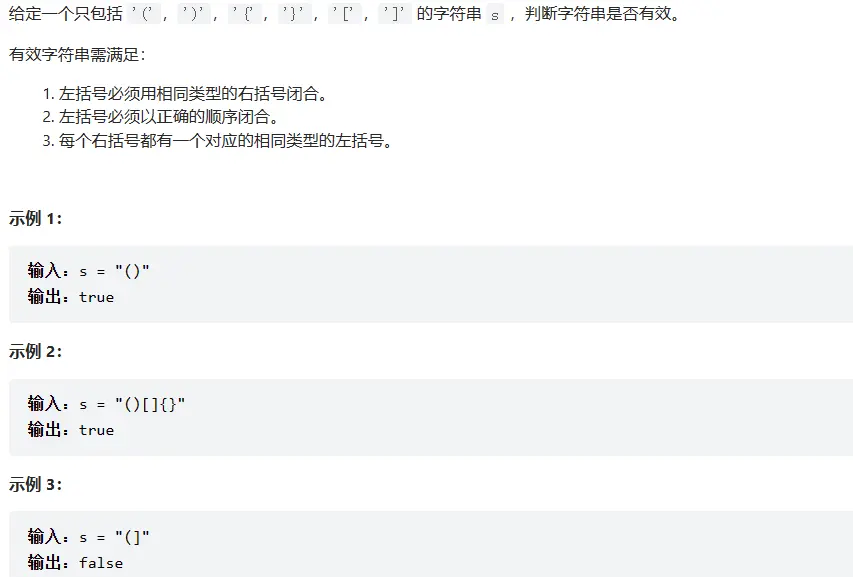
class Solution {
    public boolean isValid(String s) {
        // 用数组来做，思想和用栈做一样，但效率高
        char[] c = new char[s.length()];
        // 标记数组 c 中下一个元素应该插入的位置
        int index = 0; 
        // 遍历字符串 s 中的每个字符
        for(int i = 0; i < s.length(); i++) { 
            // 取出字符串 s 中第 i 个字符
            char c1 = s.charAt(i); 
            
            if(c1 == '(') 
                // 如果该字符是左括号 '(', 则将相应的右括号 ')' 存入数组 c 中
                c[index++] = ')';
            else if(c1 == '[') 
                // 如果该字符是左括号 '[', 则将相应的右括号 ']' 存入数组 c 中
                c[index++] = ']';
            else if(c1 == '{') 
                // 如果该字符是左括号 '{', 则将相应的右括号 '}' 存入数组 c 中
                c[index++] = '}';
            else if(index == 0 || c[--index] != c1) 
                // 如果该字符不是左括号，且该字符与数组 c 中最后一个元素不匹配，或者数组 c 中没有元素，则返回 false
                return false;
        }
        // 如果数组 c 中的所有元素都被匹配了，则返回 true，否则返回 false
        return index == 0; 
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

        int n = s.length();
        if(n % 2 == 1){
            return false;
        }
        int length = n / 2;
        for( int i = 0;i < length;i++){
            s = s.replace("()","");
            s = s.replace("[]","");
            s = s.replace("{}","");
        }
        return s.length() == 0;

1
2
3
4
5
6
7
8
9
10
11

        if(s.length() % 2 == 1){
            return false;
        }
        HashMap<Character, Character> map = new HashMap<>();
        map.put('(',')');
        map.put('[',']');
        map.put('{','}');

        char[] arr = new char[s.length()];
        int idx = 0;
        	for (char c: s.toCharArray()) {
        	if (map.containsKey(c)) {
        		arr[idx++] = c;
        		continue;
        	}
        	if (idx == 0) {
        		return false;
        	}
        	if (map.get(arr[idx-1]) == c) {
        		idx--;
        	} else {
        		return false;
        	}
        }
        return idx == 0;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 21. 合并两个有序链表 (opens new window)

# 题目描述

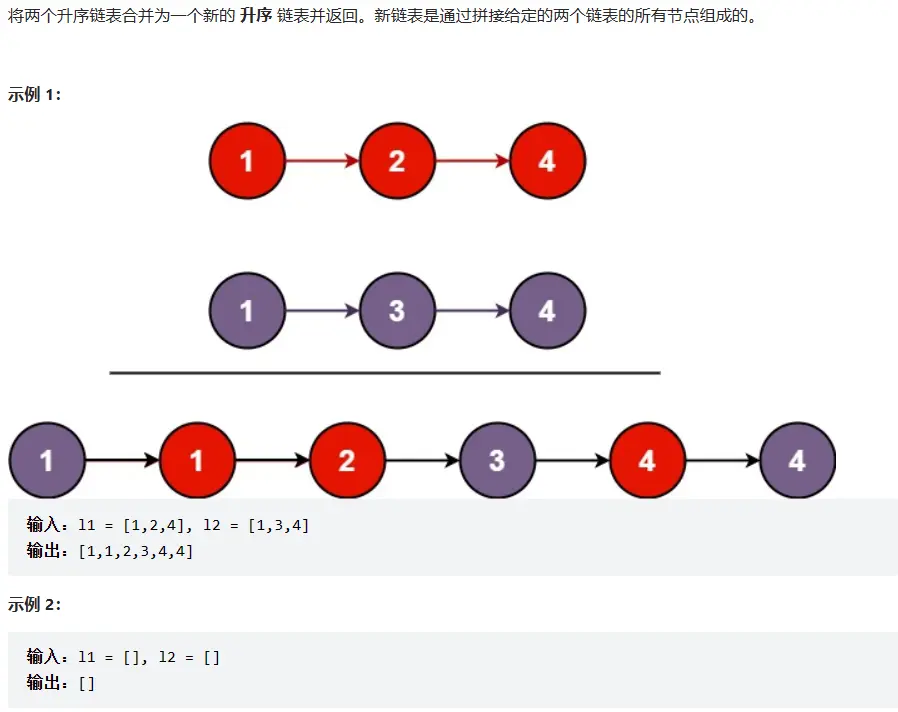
# 方法一：迭代

    /**
     * 1、迭代（双指针） -- 0ms(100.00%), 41.5MB(5.14%)
     * <p>
     * 时间复杂度：O(m + n), 其中 m 和 n 分别为两个链表的长度。
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
            ListNode res = new ListNode();
            ListNode curr = res;
            // 均不为 空 的情况
            while (list1 != null && list2 != null) {
                if (list1.val <= list2.val) {
                    curr.next = list1;
                    list1 = list1.next;
                } else {
                    curr.next = list2;
                    list2 = list2.next;
                }
                curr = curr.next;
            }
            // 至少有一个为 空 的情况
            curr.next = list1 == null ? list2 : list1;
            return res.next;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 41.62MB(5.14%)
     * <p>
     * 时间复杂度：O(m + n), 其中 m 和 n 分别为两个链表的长度。
     * <p>
     * 空间复杂度：O(m + n)
     */
    class Solution2 {
        public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
            if (list1 == null) {
                return list2;
            } else if (list2 == null) {
                return list1;
            } else if (list1.val < list2.val) {
                list1.next = mergeTwoLists(list1.next, list2);
                return list1;
            } else {
                list2.next = mergeTwoLists(list1, list2.next);
                return list2;
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

先递归，再回溯 return

# 70. 爬楼梯 (opens new window)

// 动态规划
class Solution {
    public int climbStairs(int n) {
        // 001 011 112 123 235
        int a = 0, b = 0, res = 1;

        for(int i =1; i <= n; i++) {
            a = b;
            b = res;
            res = a + b;
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 94. 二叉树的中序遍历 (opens new window)

# 题目描述

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

1
2

示例 2：

输入：root = []
输出：[]

1
2

示例 3：

输入：root = [1]
输出：[1]

1
2

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

# 方法一：递归

    /**
     * 1、递归 -- 0ms(100.00%), 40.80MB(5.08%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public List<Integer> inorderTraversal(TreeNode root) {
            // 新建一个存放遍历结果的集合
            List<Integer> res = new ArrayList<>();
            // 左根右排序 遍历
            midorder(root, res);

            // 返回遍历结果
            return res;
        }

        public void midorder(TreeNode root, List<Integer> res) {
            // 判断到空节点，直接断开
            if (root == null) {
                return;
            }
            // 递归左子树
            midorder(root.left, res);
            // 存值
            res.add(root.val);
            // 递归右子树
            midorder(root.right, res);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 方法二：栈

    /**
     * 2、栈 -- 0ms(100.00%), 40.73MB(5.29%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public List<Integer> inorderTraversal(TreeNode root) {
            // 创建结果列表，用于存储中序遍历后的值
            List<Integer> res = new ArrayList<>();
            // 创建一个栈，用于存储遍历过程中的节点
            Stack<TreeNode> stack = new Stack<>();

            // 当根节点不为空或者栈不为空时，循环继续
            while (root != null || !stack.isEmpty()) {
                // 如果根节点不为空
                if (root != null) {
                    // 将根节点入栈
                    stack.push(root);
                    // 继续遍历左子树
                    root = root.left;
                    // 否则，弹出栈顶节点，将其值添加到列表中，遍历右子树
                } else {
                    // 弹出栈顶节点
                    root = stack.pop();
                    // 将栈顶节点的值添加到列表中
                    res.add(root.val);
                    // 遍历右子树
                    root = root.right;
                }
            }

            // 返回中序遍历后的列表
            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 方法三：莫里斯遍历

    /**
     * 3、Morris(莫里斯) 实现中序遍历 -- 0ms(100.00%), 40.73MB(5.29%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public List<Integer> inorderTraversal(TreeNode root) {
            // 创建结果列表，存放中序遍历的结果
            List<Integer> res = new ArrayList<>();

            // 有根节点时，进行循环
            while (root != null) {
                // 如果根节点的左子节点为空，将根节点的值添加到列表中，然后将右子节点作为新的根节点
                if (root.left == null) {
                    res.add(root.val);
                    root = root.right;
                } else {
                    // 否则，找到根节点左子树的最右子节点（中序遍历在根节点之前的节点）
                    TreeNode prev = root.left;
                    while (prev.right != null && prev.right != root) {
                        prev = prev.right;
                    }

                    // 如果最右子节点的右子节点为空，将其右子节点设置为当前根节点，然后将左子节点作为新的根节点
                    if (prev.right == null) {
                        prev.right = root;
                        root = root.left;
                    } else {
                        // 否则（即最右子节点的右子节点为当前根节点），将根节点的值添加到列表中，将最右子节点的右子节点设为空，然后将右子节点作为新的根节点
                        res.add(root.val);
                        prev.right = null;
                        root = root.right;
                    }
                }
            }

            // 返回中序遍历的结果
            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# 图解莫里斯

参考文章：【动画模拟】二叉树神级遍历！（Morris） - 知乎 (zhihu.com) (opens new window)

# 101. 对称二叉树 (opens new window)

# 题目描述

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

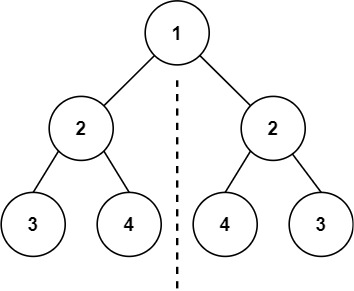
输入：root = [1,2,2,3,4,4,3]
输出：true

1
2

示例 2：

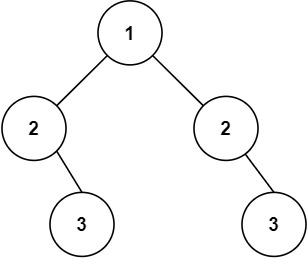
输入：root = [1,2,2,null,3,null,3]
输出：false

1
2

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

# 方法一：迭代（队列）

    /**
     * 1、迭代（队列） -- 1ms(19.18%), 40.98MB(5.02%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public boolean isSymmetric(TreeNode root) {
            if(root == null) {
                return true;
            }
            Queue<TreeNode> queue1 = new LinkedList<>();
            Queue<TreeNode> queue2 = new LinkedList<>();
            queue1.offer(root.left);
            queue2.offer(root.right);

            while (!queue1.isEmpty() && !queue2.isEmpty()) {
                TreeNode left = queue1.poll();
                TreeNode right = queue2.poll();

                if(left == null && right == null){
                    continue;
                }
                if(left == null || right == null || left.val != right.val){
                    return false;
                }

                queue1.offer(left.left);
                queue1.offer(left.right);
                queue2.offer(right.right);
                queue2.offer(right.left);
            }
            return queue1.isEmpty() && queue2.isEmpty();
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 40.89MB(5.02%)
     * <p>
     * 时间复杂度：O(n), 因为要遍历 n 个节点
     * <p>
     * 空间复杂度：O(n), 因为递归需要栈空间, 空间复杂度是递归的深度, 也就是跟树高度有关
     */
    class Solution2 {
        public boolean isSymmetric(TreeNode root) {
            return dfs(root, root);
        }

        private boolean dfs(TreeNode root1, TreeNode root2) {
            if (root1 == null && root2 == null) {
                return true;
            }
            if (root1 == null || root2 == null || root1.val != root2.val) {
                return false;
            }
            return dfs(root1.left, root2.right) && dfs(root1.right, root2.left);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 104. 二叉树的最大深度 (opens new window)

# 题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

1
2

示例 2：

输入：root = [1,null,2]
输出：2

1
2

# 方法一：队列(广度优先搜索)

    /**
     * 1、队列(广度优先搜索) -- 1ms(22.26%), 41.79MB(5.38%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public int maxDepth(TreeNode root) {
            // 判断 根节点是否为空
            if(root == null) {
                return 0;
            }
            // 建立一个新队列，存每一层的节点
            Queue<TreeNode> queue = new LinkedList<>();
            // 根节点进队列
            queue.offer(root);
            // 深度值计数
            int res = 0;

            // 循环直到队列为空
            while(!queue.isEmpty()) {
                // 这一层队列的个数
                int size = queue.size();
                // 遍历这一层所所有节点并 出队列
                while(size > 0) {
                    // 出队
                    TreeNode node = queue.poll();
                    // 左子树不为空，进队
                    if(node.left != null) {
                        queue.offer(node.left);
                    }
                    // 右子树不为空，进队
                    if(node.right != null) {
                        queue.offer(node.right);
                    }
                    size--;
                }
                // 深度+1
                res++;
            }

            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 41.63MB(11.64%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public int maxDepth(TreeNode root) {
            if (root == null) {
                return 0;
            }
            int left = maxDepth(root.left);
            int right = maxDepth(root.right);
            return Math.max(left, right) + 1;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 108. 将有序数组转换为二叉搜索树 (opens new window)

# 题目描述

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

1
2
3

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

1
2
3

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列

# 题目分析

题意：根据升序数组，恢复一棵高度平衡的 BST🌲。

分析：

BST 的中序遍历是升序的，因此本题等同于根据中序遍历的序列恢复二叉搜索树。
因此我们可以以升序序列中的任一个元素作为根节点，以该元素左边的升序序列构建左子树，以该元素右边的升序序列构建右子树，这样得到的树就是一棵二叉搜索树啦
又因为本题要求高度平衡，因此我们需要选择升序序列的中间元素作为根节点奥

# 方法一：二分 + 递归

    /**
     * 1、二分 + 递归 -- 0ms(100.00%), 41.91MB(88.88%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(logn)
     */
    class Solution {
        public TreeNode sortedArrayToBST(int[] nums) {
            return dfs(nums, 0, nums.length - 1);
        }

        private TreeNode dfs(int[] nums, int start, int end) {
            if (start > end) {
                return null;
            }
            // 以升序数组的中间元素作为根节点 root
            // start + (end - start) / 2 == (start + end) >> 1
            int mid = (start + end) >> 1;
            TreeNode root = new TreeNode(nums[mid]);
            // 递归的构建 root 的左子树与右子树
            root.left = dfs(nums, start, mid - 1);
            root.right = dfs(nums, mid + 1, end);
            // 返回构建好的根节点 root
            return root;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

学习参考：

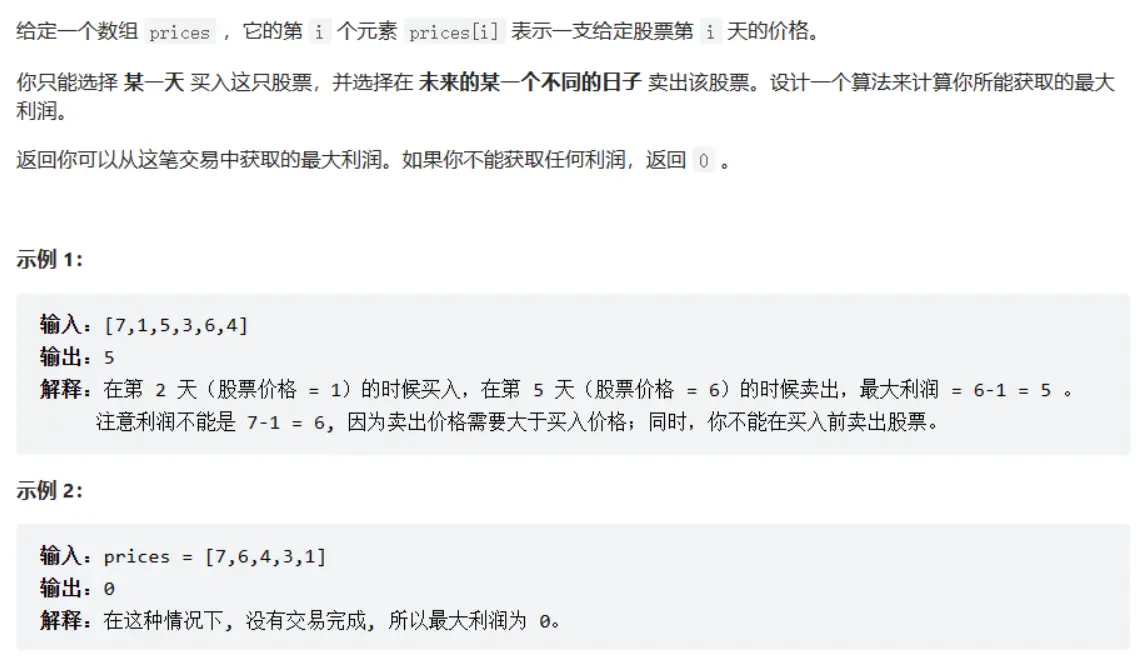
# 121. 买卖股票的最佳时机 (opens new window)

class Solution {
    public int maxProfit(int[] prices) {
        // 设置起始最小值
        int minprice = Integer.MAX_VALUE;
        // 最大利润
        int maxprofit = 0;

        for(int i = 0; i < prices.length; i++) {
            if(prices[i] < minprice) {
                minprice = prices[i];
            }else if((prices[i] - minprice) > maxprofit) {
                maxprofit = prices[i] - minprice;
            }
        }
        return maxprofit;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 136. 只出现一次的数字 (opens new window)

class Solution {
    public int singleNumber(int[] nums) {
        /*
        根据异或性质:
        1. 任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
        2. 任何数和其自身做异或运算，结果是 a⊕a=0。
        3. 异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。        
        因此将所有元素进行异或即可得到结果
         */
        int res = 0;
        for (int num : nums) {
            res ^= num;
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

可以利用 Hash 表:

class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for (Integer i : nums) {
            Integer count = map.get(i);
            count = count == null ? 1 : ++count;
            map.put(i, count);
        }
        for (Integer i : map.keySet()) {
            Integer count = map.get(i);
            if (count == 1) {
                return i;
            }
        }
        return -1; // can't find it.
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

双循环：

int singleNumber(int* nums, int numsSize){

    for(int i=0;i<numsSize;i++){
            
            int count=0;

        for(int j=0;j<numsSize;j++){
            
            if(nums[j]==nums[i])
                count++;
        }    
       
        if(count==1)
            return nums[i];
    }
    return -1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 141. 环形链表 (opens new window)

# 题目描述

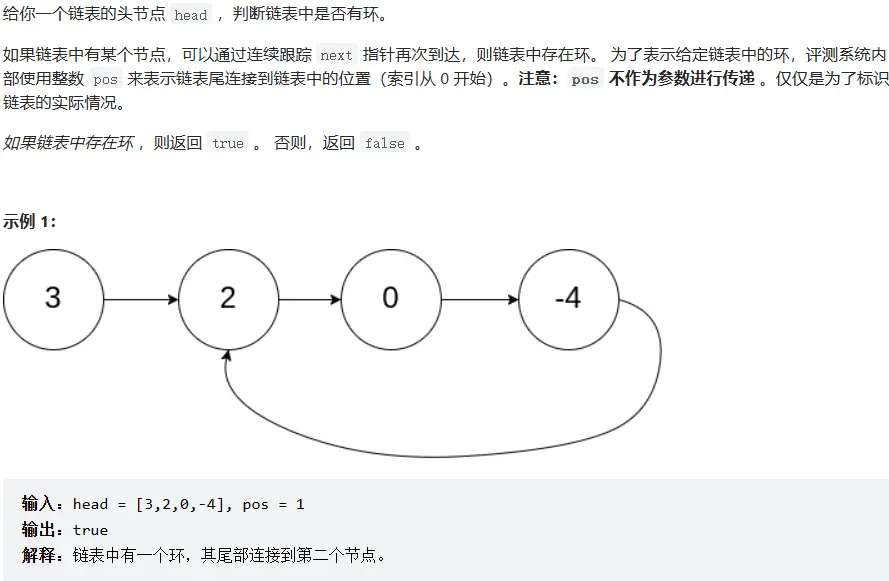
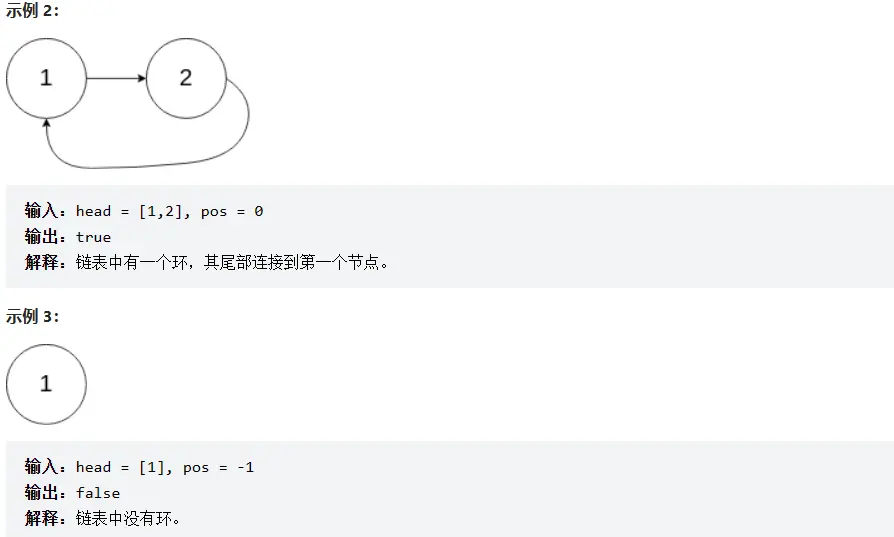
# 方法一：快慢指针

    /**
     * 1、快慢指针 -- 0ms(100.00%), 42.80MB(21.80%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    public class Solution {
        public boolean hasCycle(ListNode head) {
            if (head == null || head.next == null) {
                return false;
            }
            ListNode fast = head.next;
            ListNode slow = head;
            while(fast != null && fast.next != null) {
                fast = fast.next.next;
                slow = slow.next;
                if (fast == slow) return true;
            }
            return false;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 方法二：哈希表

    /**
     * 2、利用不重复性（HashSet） -- 4ms(13.84%), 43.90MB(5.03%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    public class Solution2 {
        public boolean hasCycle(ListNode head) {
            // 创建一个HashSet，用于存储已经访问过的节点
            Set<ListNode> seen = new HashSet<ListNode>();
            while(head != null) {
                // 如果HashSet中已经存在当前节点，则说明有环
                if(!seen.add(head)){
                    return true;
                }
                head = head.next;
            }
            return false;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 160. 相交链表 (opens new window)

# 题目描述

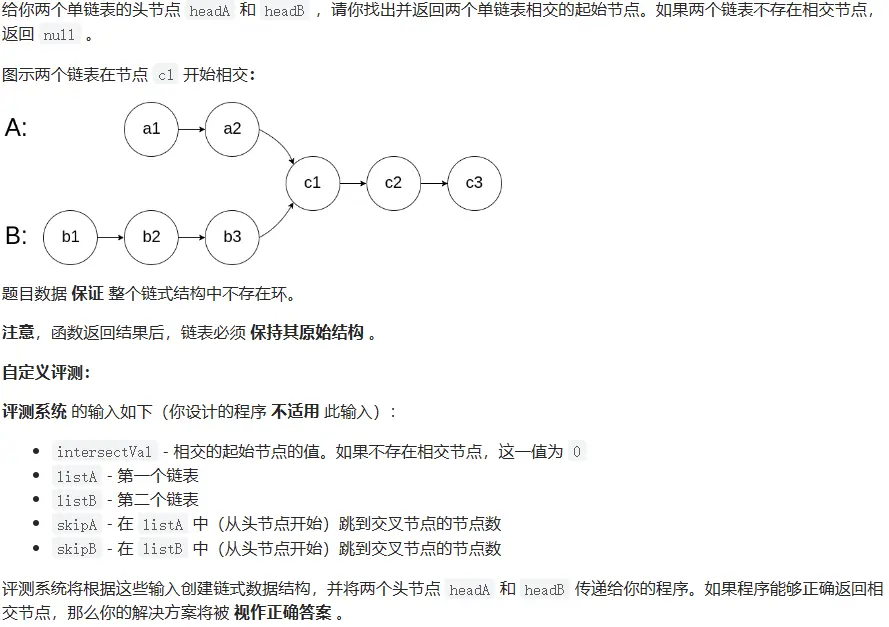
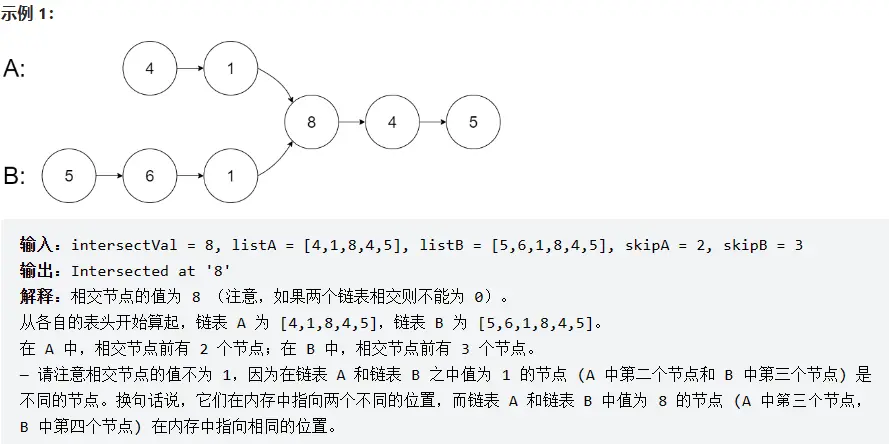
# 方法一：遍历 + HashSet

    /**
     * 1、遍历 + HashSet -- 6ms(13.58%), 46.7MB(5.00%)
     * <p>
     * 时间复杂度：O(m + n), 其中 m 和 n 分别是 headA 和 headB 的长度。
     * <p>
     * 空间复杂度：O(m), HashSet 存储的是 headA 的所有节点
     */
    public class Solution {
        public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
            Set<ListNode> hashSet = new HashSet<>();
            // 先遍历A链表,并把A链表的所有节点加入到哈希集合中
            ListNode temp = headA;
            while (temp != null) {
                hashSet.add(temp);
                temp = temp.next;
            }
            // 再遍历B链表
            temp = headB;
            while (temp != null) {
                // 判断集合中是否包含B链表的此节点
                if (hashSet.contains(temp)) {
                    // 包含，返回相交节点
                    return temp;
                }
                // 不包含，遍历下一个节点
                temp = temp.next;
            }
            // 没有相交节点，返回null
            return null;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 方法二：双指针

思路分析：

pA遍历 a+c+b 次 pB遍历 b+c+a 次

pA == pB 即可得到相交节点

    /**
     * 2、双指针 -- 1ms(99.09%), 47.42MB(5.00%)
     * <p>
     * 时间复杂度：O(m + n), 其中 m 和 n 分别是 headA 和 headB 的长度。
     * <p>
     * 空间复杂度：O(1)
     */
    public class Solution {
        public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
            ListNode a = headA, b = headB;
            while (a != b) {
                a = a == null ? headB : a.next;
                b = b == null ? headA : b.next;
            }
            return a;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 169. 多数元素 (opens new window)

class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for (Integer i : nums) {
            Integer count = map.get(i);
            count = count == null ? 1 : ++count;
            map.put(i, count);
        }
        for (Integer i : map.keySet()) {
            Integer count = map.get(i);
            if (count > nums.length/2) {
                return i;
            }
        }
        return -1;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 206. 反转链表 (opens new window)

# 题目描述

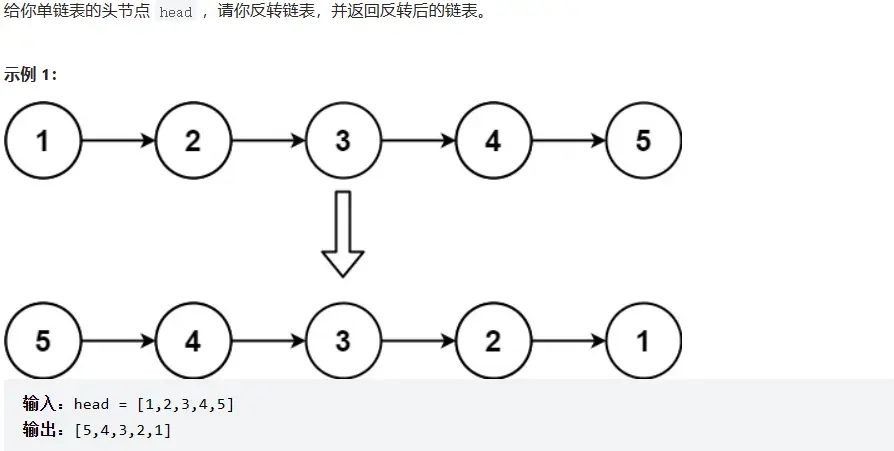
# 方法一：双指针

    /**
     * 1、迭代（双指针） -- 0ms(100.00%), 41.18MB(5.01%)
     * <p>
     * 时间复杂度：O(n), 其中 n 为链表的长度。
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public ListNode reverseList(ListNode head) {
            // 假设最前面是个null
            ListNode prev = null;
            // 当前节点，初始值为头节点。
            ListNode curr = head;

            // 遍历链表，每遍历一次就转换一次箭头
            while (curr != null) {
                // 存储当前节点（头节点）的下一节点
                ListNode next = curr.next;
                // null（prev）->curr 变为 null（prev）<-curr，转换箭头
                curr.next = prev;
                // 前置指针后移一位
                prev = curr;
                // 后置指针后移一位
                curr = next;
            }
            return prev;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 41.30MB(5.01%)
     * <p>
     * 时间复杂度：O(n), 其中 n 为链表的长度。
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution2 {
        public ListNode reverseList(ListNode head) {
            // 空链表 或者 尾结点
            if(head == null || head.next == null) {
                return head;
            }
            // 递归
            ListNode res = reverseList(head.next);
            // 反转箭头
            head.next.next = head;
            // 每一节点指向null，把null放最后
            head.next = null;

            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 226. 翻转二叉树 (opens new window)

# 题目描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

1
2

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

1
2

示例 3：

输入：root = []
输出：[]

1
2

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

# 方法一：递归

    /**
     * 1、递归（DFS） -- 0ms(100.00%), 40.19MB(5.04%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public TreeNode invertTree(TreeNode root) {
            if (root == null) {
                return null;
            }

            // 递归左子树
            TreeNode left = invertTree(root.left);
            // 递归右子树
            TreeNode right = invertTree(root.right);

            // 翻转
            root.left = right;
            root.right = left;
            return root;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 方法二：队列

层序遍历

    /**
     * 2、队列（BFS） -- 0ms(100.00%), 40.00MB(17.56%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution2 {
        public TreeNode invertTree(TreeNode root) {
            if (root == null) {
                return null;
            }
            // Queue<TreeNode> queue = new LinkedList<>();
            Queue<TreeNode> queue = new ArrayDeque<>();
            queue.offer(root);

            while (!queue.isEmpty()) {
                TreeNode cur = queue.poll();

                TreeNode temp = cur.left;
                cur.left = cur.right;
                cur.right = temp;

                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }

            return root;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 方法三：栈

    /**
     * 3、栈（DFS） -- 0ms(100.00%), 40.21MB(5.04%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution3 {
        public TreeNode invertTree(TreeNode root) {
            if (root == null) {
                return null;
            }
            Stack<TreeNode> stack = new Stack<>();
            stack.push(root);

            while (!stack.isEmpty()) {
                TreeNode cur = stack.pop();
              
                TreeNode tmp = cur.left;
                cur.left = cur.right;
                cur.right = tmp;

                if (cur.left != null) {
                    stack.push(cur.left);
                }
                if (cur.right != null) {
                    stack.push(cur.right);
                }
            }

            return root;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 234. 回文链表 (opens new window)

# 题目描述

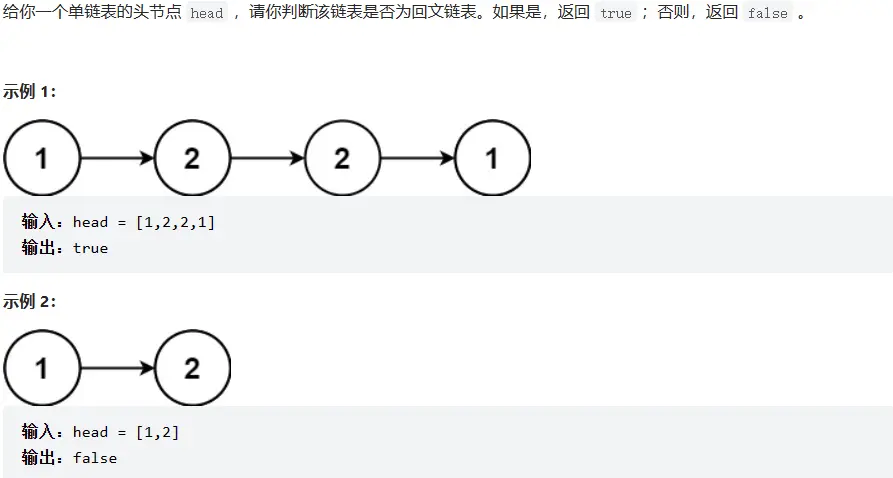
# 方法一：遍历 + 数组

    /**
     * 1、遍历 + 数组 -- 4ms(79.41%), 55.22MB(84.99%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public boolean isPalindrome(ListNode head) {
            // 空链表或仅包含一个元素的链表无论如何都是回文的（题目描述必定不为空）
            // if (head == null || head.next == null) {
            //     return true;
            // }
            int len = 0;
            ListNode p = head;
            // 得出链表长度
            while (p != null) {
                len++;
                p = p.next;
            }
            // 定义一个与链表一样长的数组
            int[] arr = new int[len];
            // 重新定义一下链表，因为上面定义的已经为空
            p = head;
            for (int i = 0; i < len; i++) {
                arr[i] = p.val;
                p = p.next;
            }
            for (int i = 0; i < len / 2; i++) {
                if (arr[i] != arr[len - 1 - i]) {
                    return false;
                }
            }
            return true;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# 方法二：遍历 + 列表

    /**
     * 2、遍历 + 列表 -- 8ms(37.68%), 54.37MB(97.42%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public boolean isPalindrome(ListNode head) {
            List<Integer> list = new ArrayList<>();
            while (head != null) {
                list.add(head.val);
                head = head.next;
            }
            int mid = list.size() >> 1;
            for (int left = 0; left < mid; left++) {
                if (list.get(left) != list.get(list.size() - 1 - left)) {
                    return false;
                }
            }
            return true;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 方法三：快慢指针 + 反转链表

    /**
     * 3、快慢指针 + 反转链表 -- 4ms(79.41%), 67.43MB(5.6%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public boolean isPalindrome(ListNode head) {
            if (head == null || head.next == null) {
                return true;
            }

            // 使用快慢指针找到链表的中点
            ListNode slow = head;
            ListNode fast = head;
            while (fast.next != null && fast.next.next != null) {
                slow = slow.next;
                fast = fast.next.next;
            }

            // 反转链表的后半部分
            ListNode secondHalf = reverseList(slow.next);
            slow.next = null;

            // 比较前半部分和反转后的后半部分
            ListNode p1 = head;
            ListNode p2 = secondHalf;
            while (p1 != null && p2 != null) {
                if (p1.val != p2.val) {
                    return false;
                }
                p1 = p1.next;
                p2 = p2.next;
            }

            return true;
        }

        private ListNode reverseList(ListNode head) {
            ListNode prev = null;
            ListNode current = head;
            while (current != null) {
                ListNode nextNode = current.next;
                current.next = prev;
                prev = current;
                current = nextNode;
            }
            return prev;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

# 283. 移动零 (opens new window)

# 题目描述

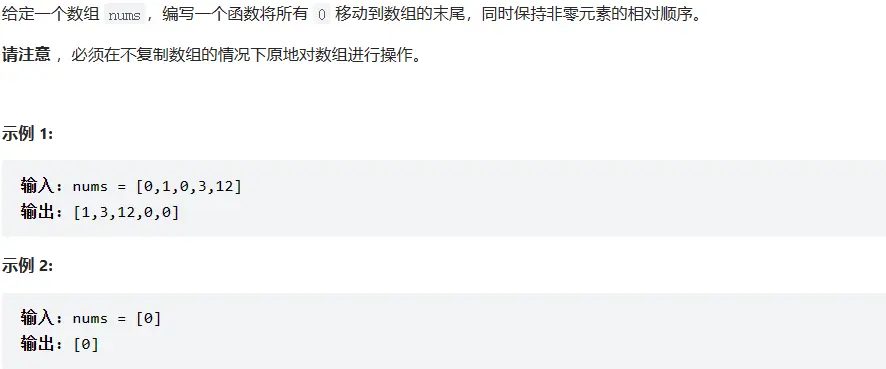
# 方法一：位置交换

    /**
     * 1、位置交换 -- 1ms(99.96%), 44.23MB(16.49%)
     * <p>
     * 时间复杂度分析：由于只对数组进行了一次遍历，所以时间复杂度为 O(n)，其中 n 是数组的长度。
     * <p>
     * 空间复杂度分析：除了输入数组之外，没有使用额外的数据结构来存储信息，因此空间复杂度为 O(1)。
     */
    class Solution {
        public void moveZeroes(int[] nums) {
            // j用来记录非0元素的索引
            int j = 0;
            // 遍历数组
            for (int i = 0; i < nums.length; i++) {
                // 如果当前元素不为0
                if (nums[i] != 0) {
                    // 记录当前元素
                    int tmp = nums[j];
                    // 将当前元素赋值给非0元素的索引
                    nums[j] = nums[i];
                    // 将记录的当前元素赋值给当前元素
                    nums[i] = tmp;
                    // 非0元素的索引加1
                    j++;
                }
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 方法二：新数组拷贝到原数组

    /**
     * 2、新数组拷贝到原数组 -- 1ms(99.96%), 43.45MB(98.82%)
     * <p>
     * 时间复杂度：总的时间复杂度为两个循环的时间复杂度之和，即 O(n + n) = O(2n)。
     * 空间复杂度为：由于创建了一个新的数组 arr 来存储非零元素，所以空间复杂度为 O(n)，其中 n 是数组的长度。
     */
    class Solution {
        public void moveZeroes(int[] nums) {

            int[] arr = new int[nums.length];
            int count = 0;
            // 遍历数组nums，将非0元素放入新的数组arr中
            for (int i = 0; i < nums.length; i++) {
                if (nums[i] != 0) {
                    arr[count] = nums[i];
                    count++;
                }
            }
            // 将新数组arr中的剩余位置都赋值为0
            for (int j = count; j < nums.length; j++) {
                arr[j] = 0;
            }
            // 将新数组arr的值拷贝到原数组nums中
            // nums = Arrays.copyof(arr,arr.length);
            System.arraycopy(arr, 0, nums, 0, arr.length);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 338. 比特位计数 (opens new window)

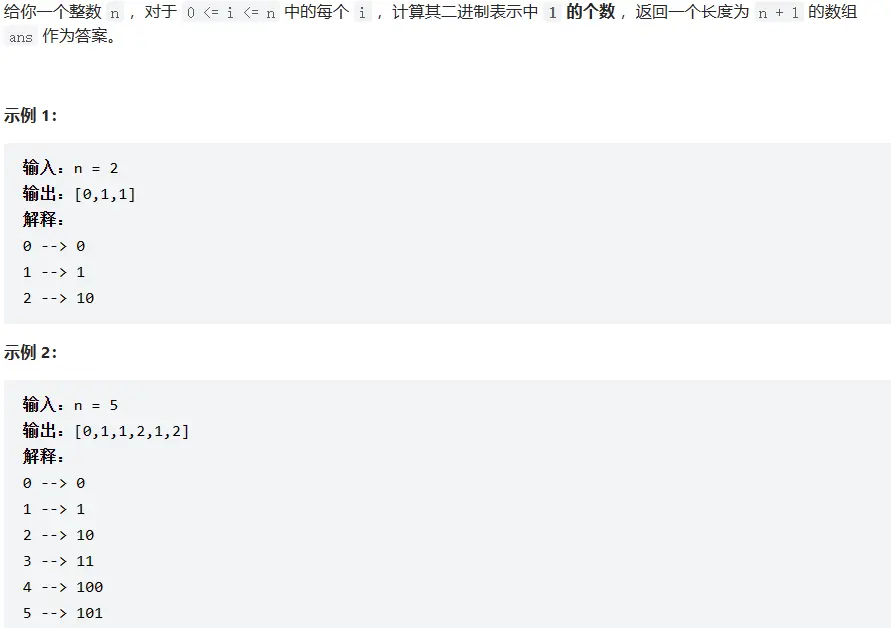
最高有效位：

class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        // 最高有效位
        int highBit = 0;
        for(int i = 1; i <= n; i++) {
            // 判断 i是否是2的幂次方，如果数字i是2的幂次方(10,100)，则它的二进制表示中只有最高位是1，其余位都是0
            if((i & (i - 1)) == 0) {
                // 如果是，更新当前最高位（它的二进制表示中只有最高位是1，其余位都是0）
                highBit = i;
            }
            // 如果当前数字i是2的幂次方，那么它的二进制中1的个数为1；（此时最高位是自己，bits[0] + 1）
            // 否则，它的二进制中1的个数等于它去掉最高位1(110 -> 10)后的数字的二进制中1的个数加1
            bits[i] = bits[i - highBit] + 1;
        }
        return bits;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

(i & (i - 1)) == 0是一个位运算的判断条件，它的含义是：如果数字i是2的幂次方，则它的二进制表示中只有最高位是1，其余位都是0。因此，当我们将i与i-1进行按位与运算时，如果结果为0，则说明i的二进制表示中只有一个1，即i是2的幂次方。这是因为，当i是2的幂次方时，i-1的二进制表示中的所有位都是1，因此按位与运算之后得到的结果为0；而当i不是2的幂次方时，i-1的二进制表示中会有一些位是0，按位与运算之后得到的结果就不为0。在这段代码中，我们使用这个条件来判断当前数字i是否是2的幂次方，如果是，则更新当前的最高位为该数字；否则，根据上述算法计算当前数字的二进制中1的个数。因此，这个判断条件在这个算法中起到了很重要的作用。
class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            bits[i] = bits[i >> 1] + (i & 1);
        }
        return bits;
    }
}
1
2
3
4
5
6
7
8
9
这也是一个计算数字0到n的二进制中1的个数的算法，具体来说，我们可以通过位运算来计算每个数字的二进制中1的个数。具体来说，对于一个数字i，我们可以将其右移一位，并将结果赋值给bits[i]，然后再判断i的二进制表示中的最低位是否为1，如果是，则将bits[i]加1。例如，对于数字6（二进制表示为110），我们将其右移一位得到3（二进制表示为11），此时bits[6]的值为bits[3]的值；然后我们再判断6的二进制表示中的最低位是否为1，发现是，因此需要将bits[6]加1，最终bits[6]的值为2。这个算法的时间复杂度为O(n)，空间复杂度为O(n)。需要注意的是，这个算法比上一个算法要更加简单和高效，因为它不需要使用特殊的判断条件，而是直接使用位运算来计算每个数字的二进制中1的个数。

# 448. 找到所有数组中消失的数字 (opens new window)

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        int n = nums.length;
        for(int num : nums) {
            // 计算当前数应该出现的位置，并将该位置的数加上n
            int x = (num - 1) % n;
            nums[x] += n;
        }
        List<Integer> res = new ArrayList<Integer>();
        for(int i = 0; i < n; i++) {
            // 如果某个位置的数小于n，则说明该位置对应的数字没有出现过
            if(nums[i] <= n) {
                res.add(i + 1);
            }
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 461. 汉明距离 (opens new window)

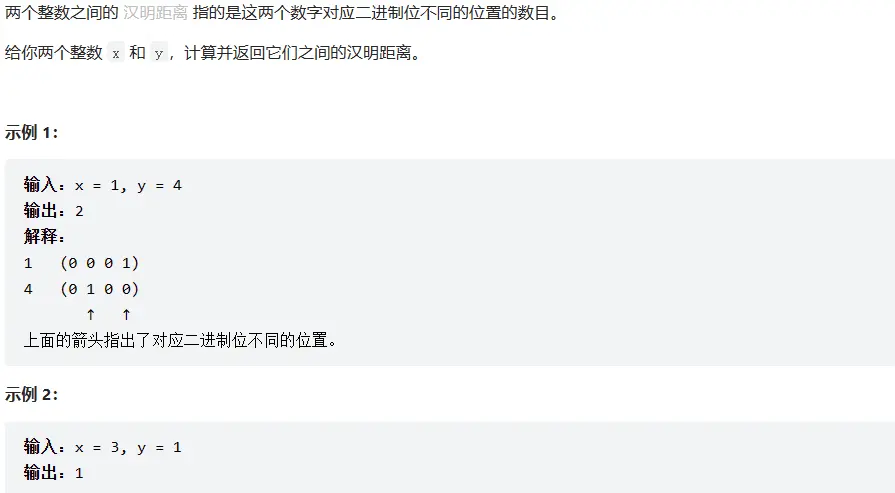
最低位：

class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while(s != 0) {
            // 累积最低位
            ret += s & 1;
            // 右移一位
            s >>= 1;
        }
        return ret;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

Interger.bitCount()：

class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y);
    }
}

1
2
3
4
5

bitCount实现的功能是计算一个（byte,short,char,int统一按照int方法计算）int,long类型的数值在二进制下“1”的数量

# 543. 二叉树的直径 (opens new window)

# 题目描述

给你一棵二叉树的根节点，返回该树的直径。

二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的长度由它们之间边数表示。

示例 1：

输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

1
2
3

示例 2：

输入：root = [1,2]
输出：1

1
2

提示：

树中节点数目在范围 [1, 104] 内
-100 <= Node.val <= 100

# 方法一：递归

    /**
     * 1、递归 -- 0ms(100.00%), 41.93MB(5.15%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        // 全局变量，统计路径节点数
        int res;

        public int diameterOfBinaryTree(TreeNode root) {
            // 二叉树的直径（最长路径上的节点数）
            res = 1;
            // 计算子树的深度
            depth(root);
            // 节点数 - 1 为边数
            return res - 1;
        }

        // 定义一个方法 depth 用来求二叉树的最大深度
        public int depth(TreeNode node) {
            // 访问到空节点了，返回0
            if (node == null) {
                return 0;
            }
            // 当前节点的左子树的深度
            int L = depth(node.left);
            // 当前节点的右子树的深度
            int R = depth(node.right);

            // 更新 ans 的值，以找到最长路径上的节点数
            res = Math.max(res, L + R + 1);

            // 返回当前节点的深度。
            return Math.max(L, R) + 1;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 617. 合并二叉树 (opens new window)

/**
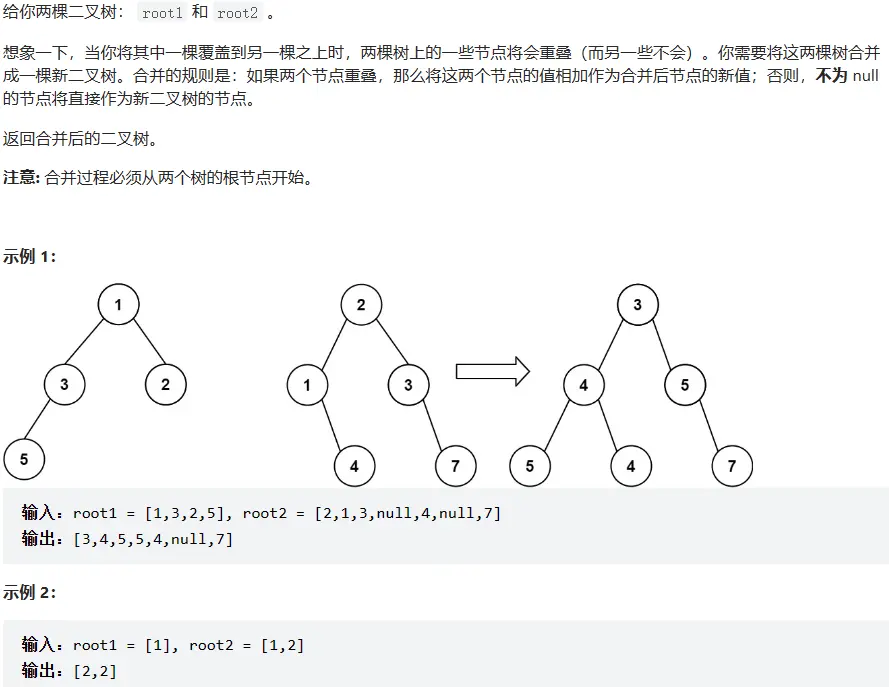
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) {
            return root2;
        }
        if (root2 == null) {
            return root1;
        }
        // 深度优先搜索
        TreeNode merged = new TreeNode(root1.val + root2.val);
        merged.left = mergeTrees(root1.left, root2.left);
        merged.right = mergeTrees(root1.right, root2.right);
        return merged;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

上次更新: 2024/9/25 11:16:13

← 解法描述中等篇（上）→