中等篇（上）

2. 两数相加 (opens new window)

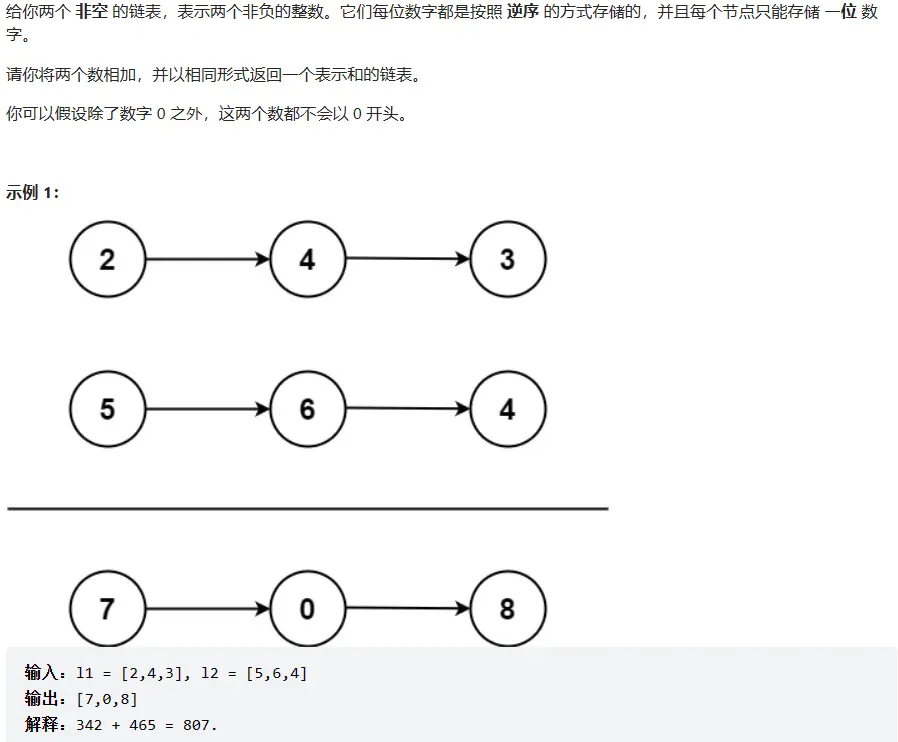
题目描述

方法一：模拟

    /**
     * 1、简约版 -- 模拟, 创建虚拟节点 -- 1ms(100%), 42.50MB(8.59%)
     *
     * 输入：l1 = [2,4,3], l2 = [5,6,4]
     * 输出：[7,0,8]
     *
     * 解释：342 + 465 = 807.
     */
    class Solution {
        public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
            // 创建一个虚拟节点
            ListNode dummy = new ListNode(0);
            // 进位
            int carry = 0;
            // 当前节点
            ListNode cur = dummy;
            // 当l1或l2不为空或者进位不为0时，循环
            while (l1 != null || l2 != null || carry != 0) {
                // 1、计算两个节点相加的值
                int s = (l1 == null ? 0 : l1.val) + (l2 == null ? 0 : l2.val) + carry;
                // 2、计算进位
                carry = s / 10;
                // 3、将计算的值赋值给当前节点
                cur.next = new ListNode(s % 10);
                // 4、将当前节点指向下一个节点
                cur = cur.next;
                // 5、将l1和l2指向下一个节点
                l1 = l1 == null ? null : l1.next;
                l2 = l2 == null ? null : l2.next;
            }
            // 返回虚拟节点的下一个节点
            return dummy.next;
        }
    }

    /**
     *  2、详细版
     *
     * 输入：l1 = [2,4,3], l2 = [5,6,4]
     * 输出：[7,0,8]
     *
     * 解释：342 + 465 = 807.
     */
    class Solution {
        public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
            // 创建一个新的链表pre，并将其头结点赋值为0，用作答案链表的头结点
            ListNode pre = new ListNode(0);
            // 创建一个指针cur，指向pre的最后一个节点
            ListNode cur = pre;
            // 进位数
            int carry = 0;

            while(l1 != null || l2 != null) {
                int x = l1 == null ? 0 : l1.val;//3 4 2
                int y = l2 == null ? 0 : l2.val;//4 6 5
                int sum = x + y + carry;//7 10 8
                // 更新进位
                carry = sum / 10;//0 1 0
                // 当前两位节点的和
                sum = sum % 10;//7 0 8
                // 将sum对10取余得到当前位节点的值，用它创建一个新的节点，并将其作为答案链表的下一个节点
                cur.next = new ListNode(sum);//7 0 8

                // 将指针cur指向新创建的节点，以便后续使用cur指针来连接下一个新节点
                cur = cur.next;//7 0 8
                if(l1 != null)
                    l1 = l1.next;//4 2
                if(l2 != null)
                    l2 = l2.next;//6 5
            }
            // 链表遍历结束后，有carry > 0，还需要在答案链表的后面附加一个节点
            if(carry == 1) {
                cur.next = new ListNode(carry);
            }
            return pre.next;
        }
    }

3. 无重复字符的最长子串 (opens new window)

题目描述

方法一：滑动窗口算法(双指针 + 哈希表)

@SuppressWarnings("all")
public class _3_无重复字符的最长子串 {

    /**
     * 1、滑动窗口解法 -- 双指针 + 哈希表 -- 7ms(28.98%), 42.81MB(21.13%)
     */
    class Solution {
        public int lengthOfLongestSubstring(String s) {
            // 创建一个哈希表，用来存储字符和位置
            HashMap<Character, Integer> map = new HashMap<>();
            // 定义 左 右 指针
            int left = 0;
            int maxLen = 0;

            // 遍历字符串
            for (int right = 0; right < s.length(); right++) {
                // 获取当前字符
                char c = s.charAt(right);
                // 如果哈希表中已经存在当前字符，则更新左指针
                if (map.containsKey(c)) {
                    left = Math.max(left, map.get(c) + 1);
                }
                // 将当前字符和位置存入哈希表
                map.put(c, right);
                // 更新最大长度
                maxLen = Math.max(maxLen, right - left + 1);
            }

            return maxLen;
        }
    }

方法二：滑动窗口(双指针 + HashSet)

    /**
     * 2、滑动窗口解法 -- 双指针 + HashSet -- 9ms(20.64%), 43MB(13.47%)
     */
    class Solution {
        public int lengthOfLongestSubstring(String s) {
            // 哈希集合，记录每个字符是否出现过
            Set<Character> hashSet = new HashSet<Character>();
            int n = s.length();

            // 右指针，初始值为-1，相当于我们在字符串的左边界的左侧，还没有开始移动
            int rk = -1, ans = 0;
            for (int i = 0; i < n; i++) {
                // 判断是否为第一个字符
                if (i != 0) {
                    // 否，左指针向右移动一格，移除一个字符
                    hashSet.remove(s.charAt(i - 1));
                }
                // 当没有越界 且 右指针的下一个字符没有出现过时
                while (rk + 1 < n && !hashSet.contains(s.charAt(rk + 1))) {
                    // 不断地移动右指针，并将该字符添加到集合 occ 中
                    hashSet.add(s.charAt(rk + 1));
                    rk++;
                }
                // 计算当前找到的最长无重复字符子串的长度，并与之前的结果取最大值
                ans = Math.max(ans, rk + 1 - i);
            }
            return ans;
        }
    }
}

5. 最长回文子串 (opens new window)

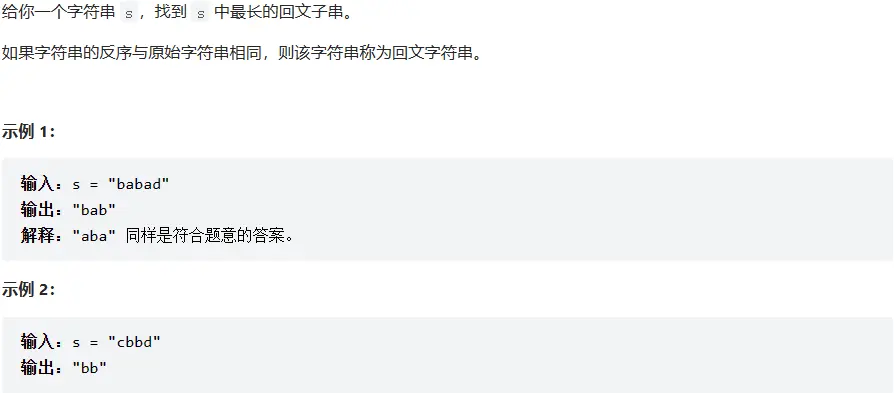
题目描述

方法一：动态规划

    /**
     * 1、动态规划 -- 131ms(34.52%), 45.06MB(9.38%)
     * <p>
     * 时间复杂度为 O(n^2), 代码中使用了两层嵌套循环来遍历整个字符串
     * <p>
     * 空间复杂度为 O(n^2), 代码中创建了一个大小为 n x n 的二维布尔数组 dp 用于存储每个位置的回文信息
     */
    class Solution {
        public String longestPalindrome(String s) {
            // 如果字符串为空或者长度小于2，则直接返回
            if (s == null || s.length() < 2) {
                return s;
            }

            // 定义字符串长度
            int strLen = s.length();
            // 定义最大回文串的起始位置
            int maxStart = 0;
            // 定义最大回文串的结束位置
            int maxEnd = 0;
            // 定义最大回文串的长度
            int maxLen = 1;

            // 定义二维数组，用于记录字符串中每个位置的回文信息
            boolean[][] dp = new boolean[strLen][strLen];

            // 右边界, 从第二个位置开始遍历字符串
            for (int right = 1; right < strLen; right++) {
                // 左边界, 从第一个位置开始遍历字符串
                for (int left = 0; left < right; left++) {
                    // 如果字符串中两个位置的字符相同，且两个位置之间的字符串长度小于等于2或者dp[left + 1][right - 1]为true，则dp[left][right]为true
                    if (s.charAt(left) == s.charAt(right)
                            && ((right - left) <= 2 || dp[left + 1][right - 1])) {
                        // 将该子串设为回文串
                        dp[left][right] = true;

                        // 如果当前回文串的长度大于最大回文串的长度，则更新最大回文串的起始位置和结束位置
                        if ((right - left + 1) > maxLen) {
                            maxLen = right - left + 1;
                            maxStart = left;
                            maxEnd = right;
                        }
                    }
                }
            }

            // 返回最大回文串, +1 是为了返回的子串包括下标为 maxEnd 的字符
            return s.substring(maxStart, maxEnd + 1);
        }
    }

方法二：暴力枚举

超出时间限制

    /**
     * 2、暴力解法 -- 超出时间限制
     * <p>
     * 时间复杂度为 O(n^3), 两层嵌套循环来枚举每个字符作为回文串的中心，然后在第三层循环中判断子串是否为回文串
     * <p>
     * 空间复杂度为 O(n^1), 代码中没有额外使用与输入字符串长度相关的空间
     */
    class Solution {

        public String longestPalindrome(String s) {
            String ans = "";
            int max = 0;
            int len = s.length();
            // 枚举每一个字符作为回文串的中心
            for (int i = 0; i < len; i++)
                for (int j = i + 1; j <= len; j++) {
                    String test = s.substring(i, j);
                    // 判断子串是否为回文串
                    if (isPalindromic(test) && test.length() > max) {
                        ans = s.substring(i, j);
                        max = Math.max(max, ans.length());
                    }
                }
            return ans;
        }

        public boolean isPalindromic(String s) {
            int len = s.length();
            // 判断子串是否为回文串
            for (int i = 0; i < len / 2; i++) {
                if (s.charAt(i) != s.charAt(len - i - 1)) {
                    return false;
                }
            }
            return true;
        }
    }

11. 盛最多水的容器 (opens new window)

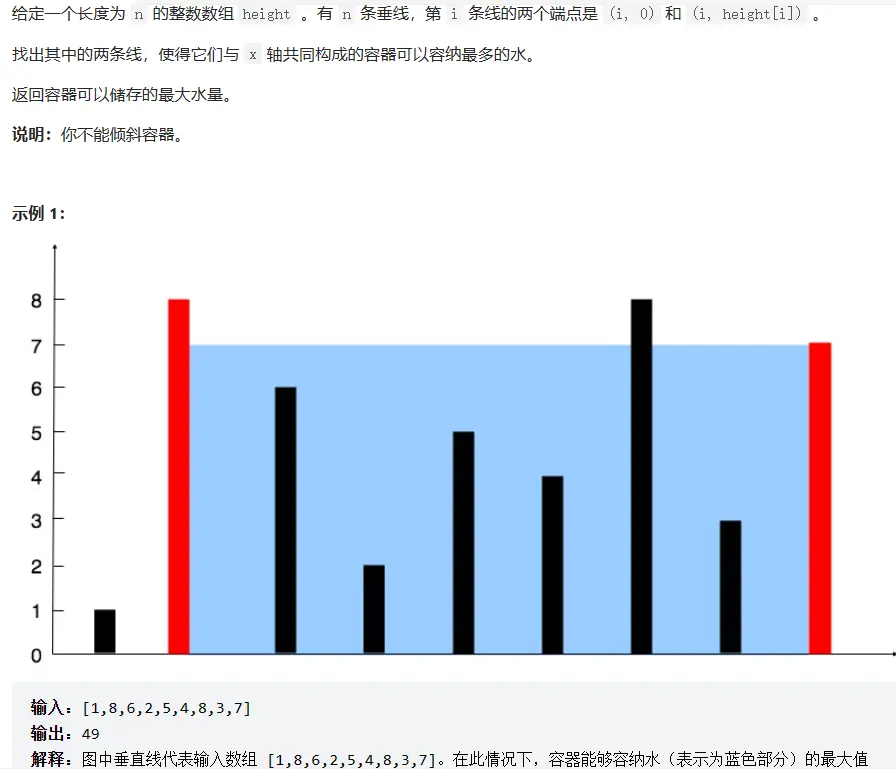
题目描述

方法一：双指针

    /**
     * 1、双指针 -- 4ms(60.90%), 54.76MB(19.09%)
     * <p>
     * 时间复杂度为 O(n)，其中n是数组height的长度。这是因为在最坏的情况下，我们需要遍历整个数组一次，每次迭代中计算面积并更新最大值的操作都是常数时间复杂度的。因此，总的时间复杂度是线性的。
     * 空间复杂度为 O(1)，因为我们只使用了固定数量的变量来存储最大面积和左右指针的位置，这些变量的空间需求不随输入数组的大小而改变。
     */
    class Solution {
        public int maxArea(int[] height) {
            // 初始化最大面积
            int max = 0;
            // 初始化左右指针
            int left = 0, right = height.length - 1;

            // 当左右指针未重合时
            while (left < right) {
                // 计算当前面积
                int area = Math.min(height[left], height[right]) * (right - left);
                // 比较当前面积和最大面积，取最大面积
                max = Math.max(max, area);

                // 移动值较小的指针
                if (height[left] < height[right]) {
                    left++;
                } else {
                    right--;
                }
            }

            // 返回最大面积
            return max;
        }
    }

15. 三数之和 (opens new window)

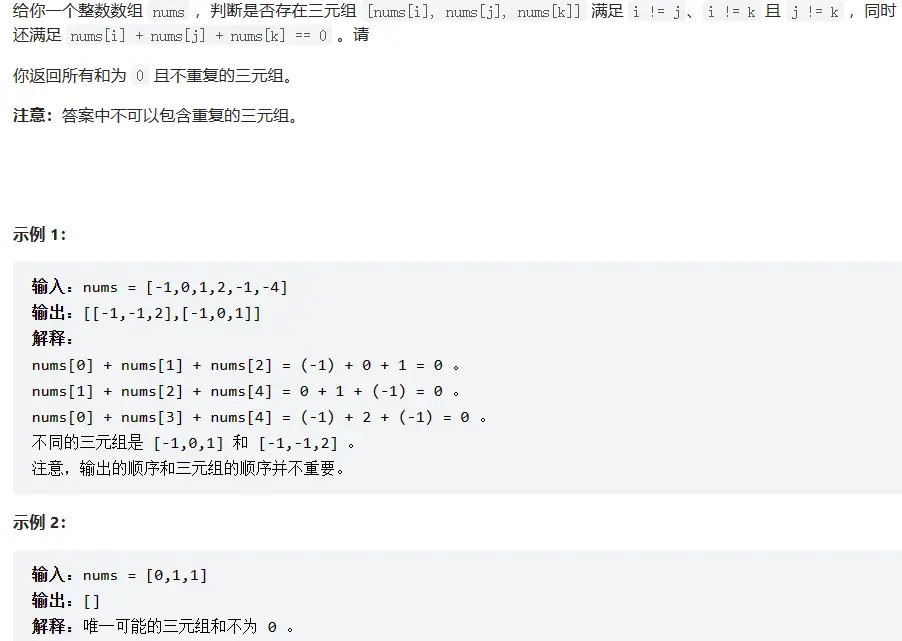
题目描述

方法一：排序 + 双指针

    /**
     * 1、排序 + 双指针 -- 30ms(80.97%), 50.38MB(18.34%)
     * <p>
     * 时间复杂度为 O(n^2)
     * 空间复杂度为 O(logn)
     */
   class Solution {
        public List<List<Integer>> threeSum(int[] nums) {
            // 对数组进行排序
            Arrays.sort(nums);
            List<List<Integer>> res = new ArrayList<>();

            int n = nums.length;
            // 遍历数组
            for (int first = 0; first < n; first++) {
                // 如果当前元素和前一个元素相等，则跳过
                if (first > 0 && nums[first] == nums[first - 1]) {
                    continue;
                }

                int third = n - 1;
                int target = -nums[first];
                // 遍历数组
                for (int second = first + 1; second < n; second++) {
                    // 如果当前元素和前一个元素相等，则跳过
                    if (second > first + 1 && nums[second] == nums[second - 1]) {
                        continue;
                    }
                    // 如果当前元素和最后一个元素相加大于target，则将third减一
                    while (second < third && nums[second] + nums[third] > target) {
                        third--;
                    }
                    // 如果second等于third，则跳出循环
                    if (second == third) {
                        break;
                    }
                    // 如果当前元素和最后一个元素相加等于target，则将当前元素、second和third添加到list中
                    if (nums[second] + nums[third] == target) {
                        List<Integer> list = new ArrayList<>();
                        list.add(nums[first]);
                        list.add(nums[second]);
                        list.add(nums[third]);
                        res.add(list);
                    }
                }
            }
            return res;
        }
    }

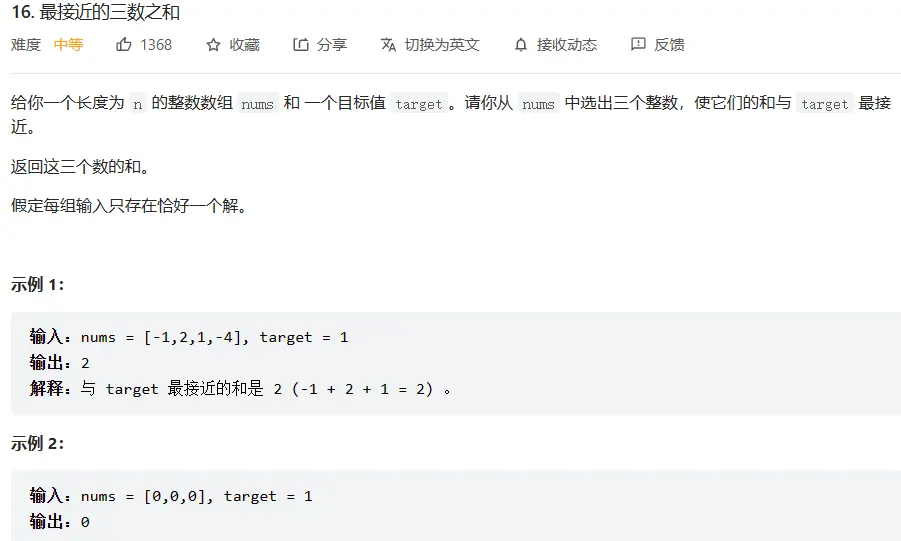
16. 最接近的三数之和 (opens new window)

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        // 先排序
        Arrays.sort(nums);
        // 获取数组长度
        int n = nums.length;
        // 前三数之和，后面用作与其他的三数之和作对比
        int ans = nums[0] + nums[1] + nums[2];
        for (int i = 0; i < nums.length; i++) {
            // 定义左右指针
            int left = i + 1, right = n - 1;
            // 直到左右指针相遇
            while (left < right) {
                // 计算和
                int sum = nums[i] + nums[left] + nums[right];
                // 比较差值
                if (Math.abs(target - sum) < Math.abs(target - ans)) {
                    ans = sum;
                }

                if (sum > target) {
                    // 当前和大于目标值，移动右指针
                    right--;
                }else if (sum < target) {
                    // 当前和小于目标值,移动左指针
                    left++;
                }else {
                    // 当前和与目标值相等,直接返回
                    return ans;
                }
            }
        }
        return ans;
    }
}

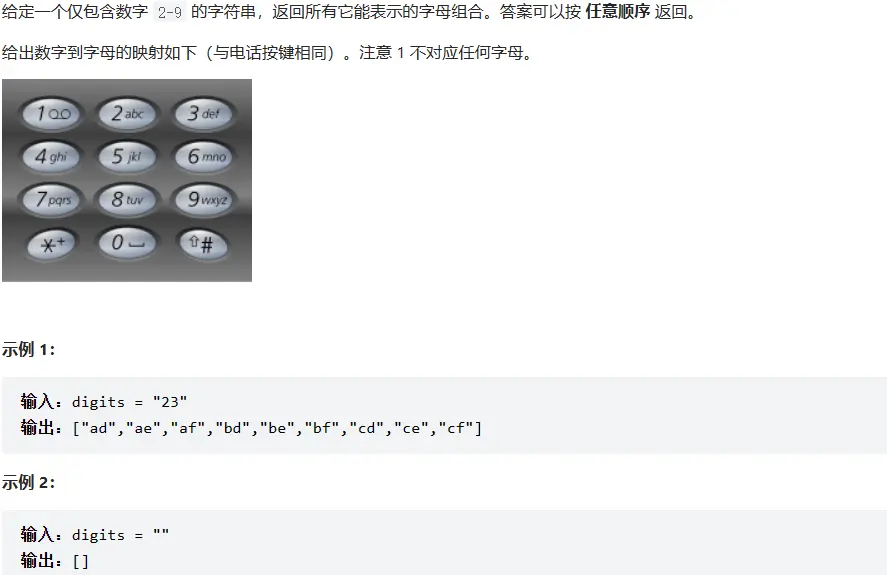
17. 电话号码的字母组合 (opens new window)

class Solution {
    public List<String> letterCombinations(String digits) {
        // 存储所有字母组合的集合
        List<String> combinations = new ArrayList<String>();
        // 空字符串直接返回空集合
        if (digits.length() == 0) {
            return combinations;
        }
        // 号码-字符串，映射存储
        Map<Character, String> phoneMap = new HashMap<Character,String>();
        phoneMap.put('2', "abc");
        phoneMap.put('3', "def");
        phoneMap.put('4', "ghi");
        phoneMap.put('5', "jkl");
        phoneMap.put('6', "mno");
        phoneMap.put('7', "pqrs");
        phoneMap.put('8', "tuv");
        phoneMap.put('9', "wxyz");
        // 回溯
        backtrack(combinations, phoneMap, digits, 0, new StringBuffer());
        return combinations;
    }

    // 递归 combination：当前的字母集合
    public void backtrack(List<String> combinations, Map<Character, String> phoneMap, String digits, int index, StringBuffer combination) {
        if (index == digits.length()) {
            // 此时枚举完了所有的数字
            combinations.add(combination.toString());// ad ae ...
        } else {
            // 提取号码数字
            char digit = digits.charAt(index);
            // 提取数字对应的字符串
            String letters = phoneMap.get(digit);
            // 对应的字符串的长度
            int lettersCount = letters.length();
            // 递归组合
             for (int i = 0; i < lettersCount; i++) {
                combination.append(letters.charAt(i));
                backtrack(combinations, phoneMap, digits, index + 1, combination);
                // 递归结束后，需要将 combination 中的最后一个字母删除，以便枚举当前数字对应的下一个字母
                // 第一次删除了 d，方便组合 ae
                combination.deleteCharAt(index);
            }
        }
    }
}

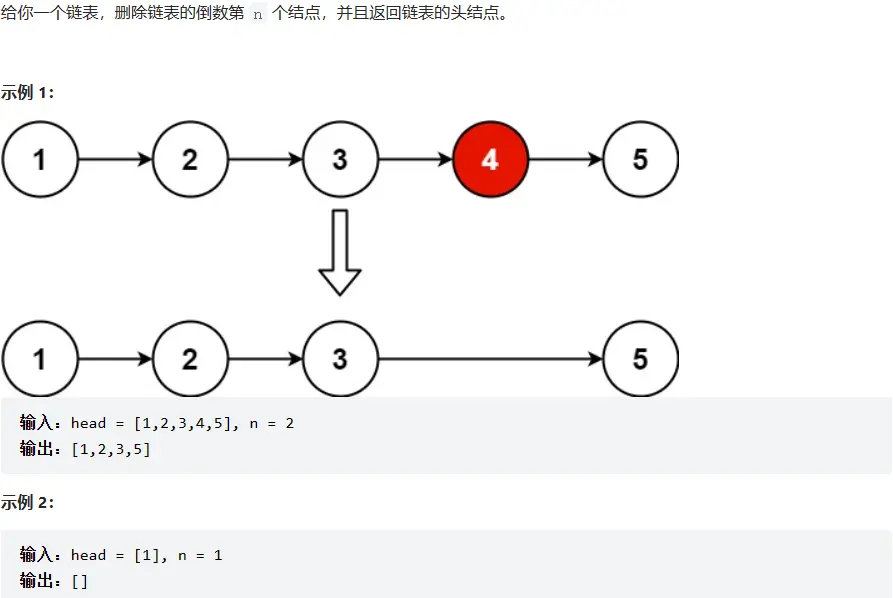
19. 删除链表的倒数第 N 个结点 (opens new window)

题目描述

方法一：虚拟头节点 + 快慢指针

    /**
     * 1、虚拟头节点 + 快慢指针 -- 0ms(100.00%), 40.54MB(12.92%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public ListNode removeNthFromEnd(ListNode head, int n) {
            // 创建一个虚拟节点，指向头节点 -- 即 dummy 为新的头节点
            ListNode dummy = new ListNode(0, head);
            // 快慢指针，快指针先走n步
            ListNode fast = dummy, slow = dummy;
            // 1、快指针先走n步
            while (n-- > 0) {
                fast = fast.next;
            }
            // 2、快慢指针同时移动，当快指针指向最后一个节点时，慢指针指向倒数第n个节点的前一个节点
            while (fast.next != null) {
                slow = slow.next;
                fast = fast.next;
            }
            // 3、删除倒数第n个节点
            slow.next = slow.next.next;
            // 返回头节点
            return dummy.next;
        }
    }

虚拟头节点的创建

参数解释如下：

1. 0：这是 ListNode 类的构造函数的第一个参数，表示节点的值。在这里，我们将其设置为 0。
2. head：这是 ListNode 类的构造函数的第二个参数，表示链表的头节点。在这里，我们将 dummy 指向 head，使得 dummy 成为链表的【新头节点】。

用途：

• 在这个特定的用法中，将整数值设置为 0，而第二个参数是 head，即原始链表的头节点。这是一种常见的技巧，通过创建一个值为 0 的虚拟头节点，可以简化一些链表操作的边界条件处理。
• 在这里是便于快慢节点的移动，快指针 移动了，不影响后续 慢指针 的移动。

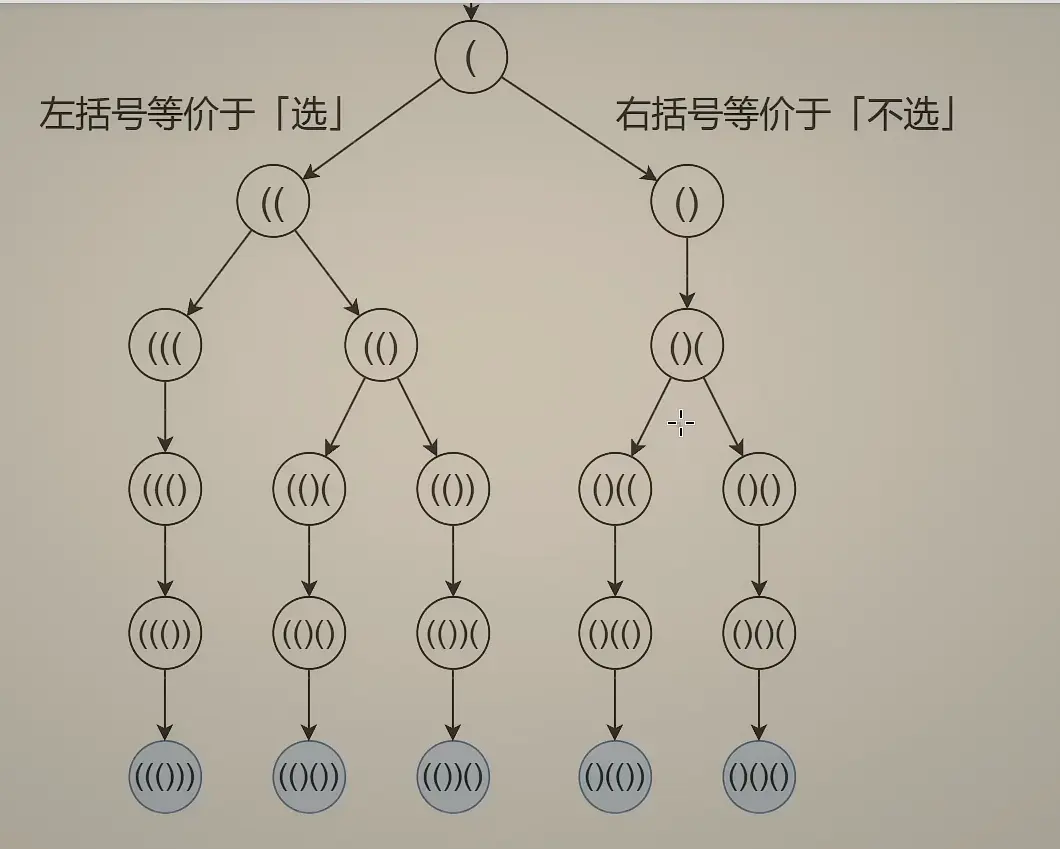
22. 括号生成 (opens new window)

class Solution {
    public List<String> generateParenthesis(int n) {
        // 定义一个结果集合
        List<String> res = new ArrayList<>();
        // 回溯
        backtrack(res, "", n, n);
        return res;
    }
    
    private void backtrack(List<String> res, String str, int left, int right) {
        // 此时已经添加了 n 个左括号和 n 个右括号，将当前字符串添加到答案列表中
        if (left == 0 && right == 0) {
            res.add(str);
            return;
        }
        // 如果剩余左括号数量大于 0，则可以添加一个左括号，并递归调用函数，将 left 减 1
        if (left > 0) {
            backtrack(res, str + "(", left - 1, right);
        }
        // 如果 right 大于 0，且 right 大于 left，则可以添加一个右括号，并递归调用函数，将 right 减 1
        if (right > 0 && right >left) {
            backtrack(res, str + ")", left, right - 1);
        }
    }
}

图解：

24. 两两交换链表中的节点 (opens new window)

题目描述：

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

• 链表中节点的数目在范围 [0, 100] 内
• 0 <= Node.val <= 100

方法一：递归

    /**
     * 1、递归 -- 0ms(100.00%), 40.40MB(5.13%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public ListNode swapPairs(ListNode head) {
            // 如果链表为空或只有一个节点，直接返回头节点，不需要进行交换
            if (head == null || head.next == null) {
                return head;
            }
          
            // 递归调用swapPairs函数，处理剩余的节点，传入头【节点的下一个节点的下一个节点】，返回值赋值给tmp
            ListNode tmp = swapPairs(head.next.next);
            // 获取当前节点的下一个节点赋值给p
            ListNode p = head.next;
          
            // 将下一个节点的next指针指向当前节点，完成交换
            p.next = head;
            // 将当前节点的next指针指向递归调用的结果，继续处理剩余的节点
            head.next = tmp;
          
            // 返回交换后的头节点
            return p;
        }
    }

代码解析

这个函数的作用是将链表中的每两个相邻节点进行交换，并返回新的头节点。具体步骤如下：

1. 首先判断链表是否为空或只有一个节点，如果是，则直接返回头节点，因为不需要交换。
2. 然后递归调用 swapPairs 函数，传入参数为当前节点的下一个节点的下一个节点（即跳过了两个节点）。这样可以处理剩余的节点。
3. 接下来，获取当前节点的下一个节点，并将其赋值给变量 p。
4. 将 p 的 next 指针指向当前节点，完成两个节点的交换。
5. 将当前节点的 next 指针指向递归调用的结果，即交换后的剩余节点。
6. 最后返回交换后的头节点 p。

通过递归调用，该函数会逐层向下处理链表，直到到达链表末尾。在每一层递归中，都会交换相邻的两个节点，并将结果传递给下一层递归。最终，当递归到最底层时，所有相邻节点都被成功交换，然后逐层向上返回，最终得到交换后的链表。

图解

示例一：

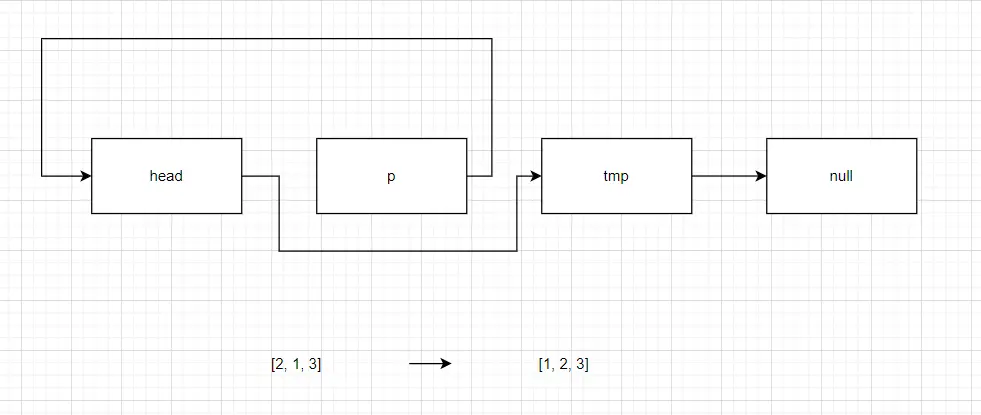
示例二：

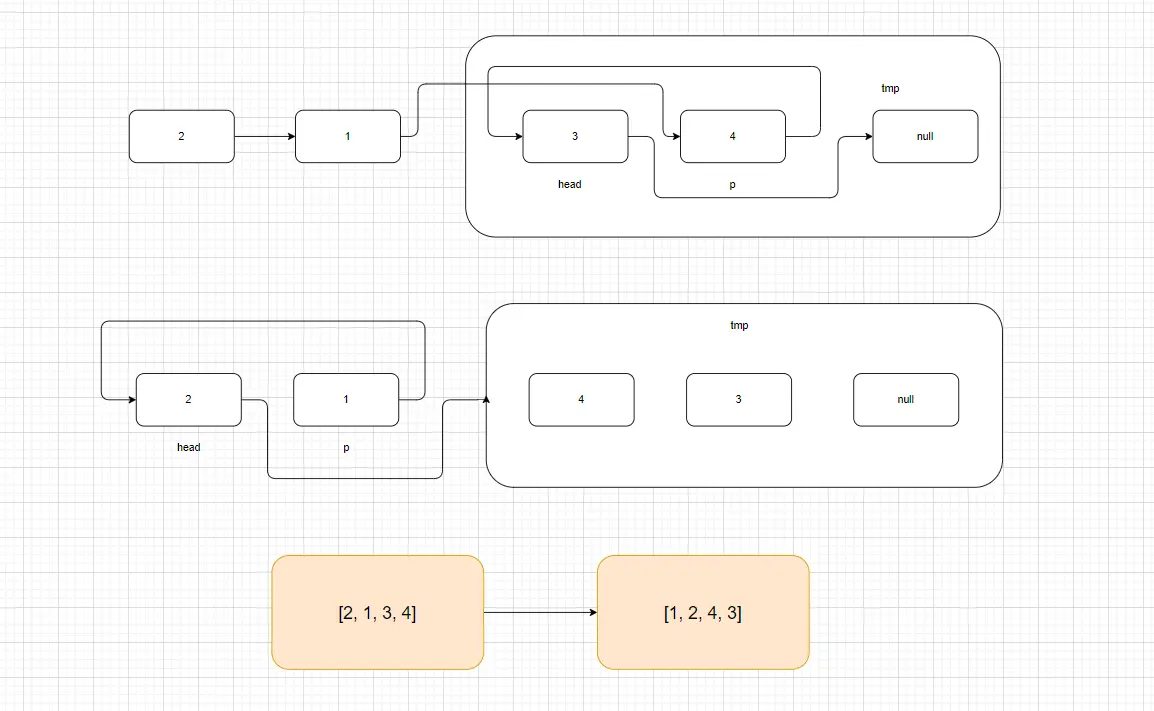
方法二：虚拟头节点 + 双指针

    /**
     * 2、虚拟头节点 + 双指针 -- 0ms(100.00%), 39.89MB(19.62%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution2 {
        public ListNode swapPairs(ListNode head) {
            // 创建虚拟头节点，并将其 next 指向原始链表的头节点
            ListNode dummy = new ListNode(0, head);
            // 创建两个指针 pre 和 cur，将 pre 初始化为虚拟头节点
            ListNode pre = dummy;
            // 将 cur 初始化为原始链表的头节点而不是虚拟头节点
            ListNode cur = head;

            // 循环条件：当前节点 cur 和它的下一个节点 cur.next 均不为 null, 不为 null 才能进行交换
            while (cur != null && cur.next != null) {
                // 创建临时节点 tmp，保存下一个节点的引用
                ListNode tmp = cur.next;
              
                // 将当前节点 cur 的 next 指针指向下一个节点的下一个节点，跳过下一个节点
                cur.next = tmp.next;
                // 将临时节点 tmp 的 next 指针指向当前节点 cur，完成交换
                tmp.next = cur;
                // 将前一个节点 pre 的 next 指针指向交换后的新节点 tmp
                pre.next = tmp;

                // 将 pre 移动到下一对相邻节点的前一个节点，即当前节点 cur
                pre = cur;
                // 将 cur 移动到下一对相邻节点的当前节点，即下一个节点
                cur = cur.next;
            }

            // 返回虚拟头节点 dummy 的 next，即完成相邻节点的交换后的链表
            return dummy.next;
        }
    }

代码解析

• 算法通过维护一个虚拟头节点，利用两个指针 pre 和 cur 在链表中遍历，不断交换相邻的节点。

• 这种方式可以避免对头节点的特殊处理

• 循环里主要是三个步骤：报存引用、更换 next 指针指向、移动指针

图解

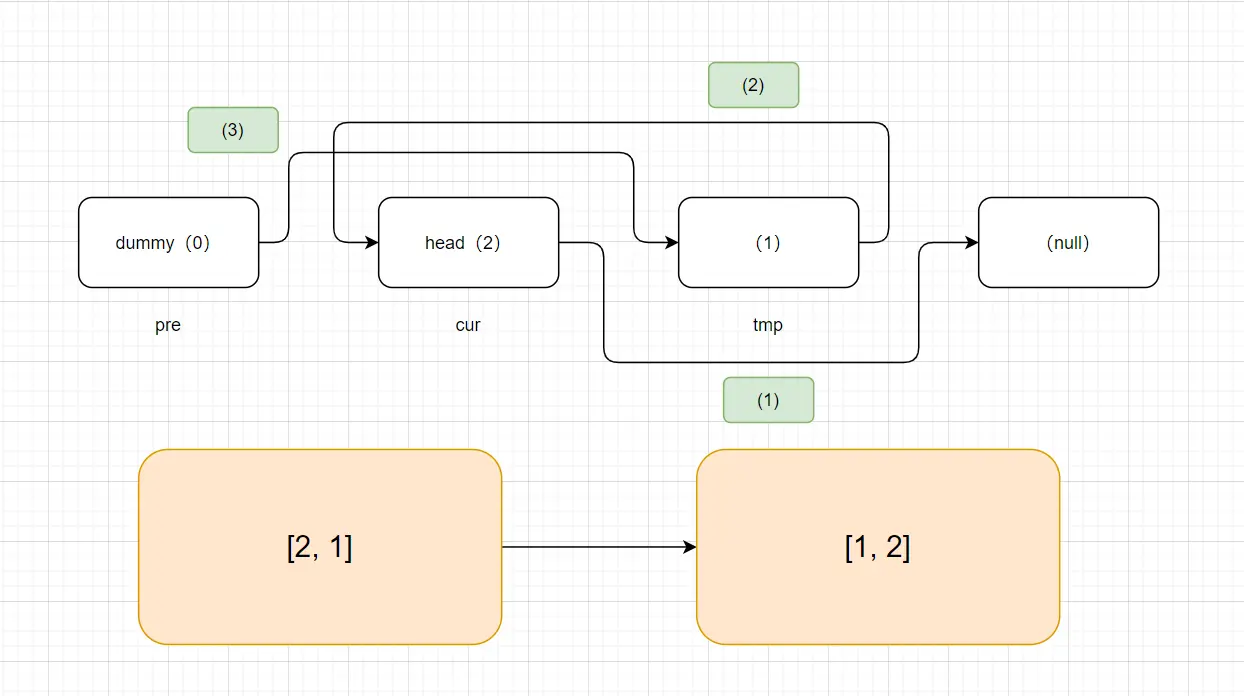
31. 下一个排列 (opens new window)

class Solution {
    public void nextPermutation(int[] nums) {
        // 从倒数第二个数开始向前遍历
        int i = nums.length - 2;
        // 找到第一个非逆序的数
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            i--;
        }
        // 如果存在非逆序数
        if (i >= 0) {
            // 从最后一个数开始向前遍历
            int j = nums.length - 1;
            // 找到比 非逆序数 大的最小数
            while (j >= 0 && nums[i] >= nums[j]) {
                j--;
            }
            // 交换 非逆序数 和 比非逆序数大的最小数
            swap(nums, i, j);
        }
        // 反转非逆序数之后的数字
        reverse(nums, i + 1);
    }

    // 交换数组中的两个位置
    public void swap(int[] nums, int i,int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    // 反转数组中 start 位置之后的数字
    public void reverse(int[] nums, int start) {
        int left = start, right = nums.length - 1;
        while (left < right) {
            swap(nums, left , right);
            left++;
            right--;
        }
    }
}

该算法的思路如下：

1. 从右往左遍历数组，找到第一个非逆序的数，记为非逆序数；

2. 如果不存在非逆序数，说明整个数组是逆序的，直接反转整个数组即可；

3. 如果存在非逆序数，从右往左找到比非逆序数大的最小数，将两个数交换位置；

4. 最后，将非逆序数之后的数字反转。 例如：给定数组[1, 3, 5, 4, 2]，下一个排列为[1, 4, 2, 3, 5]。 具体实现细节见代码中的注释。

33. 搜索旋转排序数组（二分查找） (opens new window)

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        // 数组为空，返回 -1
        if (n == 0) {
            return -1;
        }
        // 数组只有一个元素，判断是否为目标值
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        int left = 0, right = n - 1;
        // 二分查找
        while (left <= right) {
            int mid = (left + right) / 2;
            // 找到目标值，返回下标
            if (nums[mid] == target) {
                return mid;
            }
            
            if(nums[0] <= nums[mid]) { // 左半部分有序
                // 目标值在左半部分
                if (nums[0] <= target && target < nums[mid]) {
                    right = mid - 1;
                } else { // 目标值在右半部分
                    left = mid + 1;
                }
            } else { // 右半部分有序
                // 目标值在右半部分
                if (nums[mid] < target && target <= nums[n - 1]) {
                    left = mid + 1;
                } else { // 目标值在左半部分
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
}

为什么必须满足条件 nums[0] <= target ？

为了确保目标值在左半部分

假设输入[4,5,6,7,0,1,2] 0，此时target < nums[mid] == 7 但是 nums[0] == 4 > target，将会错判 0 在左边

34. 在排序数组中查找元素的第一个和最后一个位置 (opens new window)

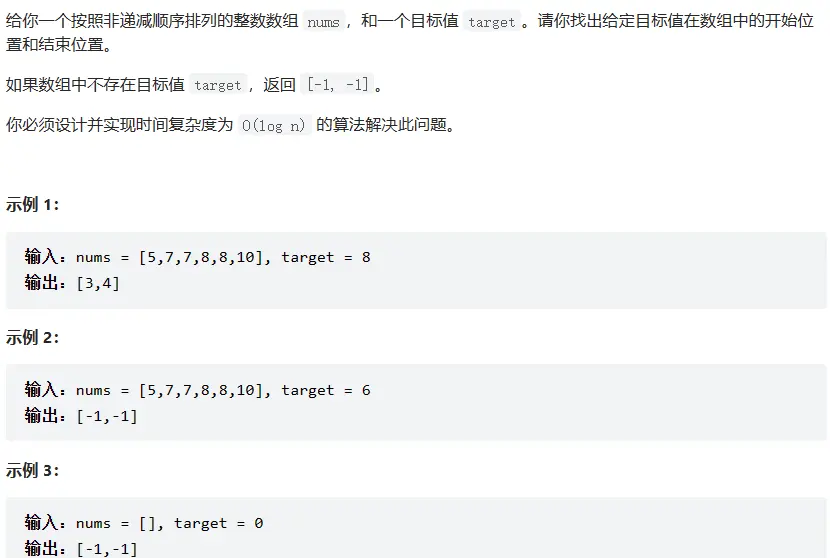
class Solution { // 时间复杂度 O(n)
    public int[] searchRange(int[] nums, int target) {
        int[] res = {-1,-1};
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == target) {
                res[0] = i;
                break;
            }
        }
        for (int j = nums.length - 1; j >= 0; j--) {
            if (nums[j] == target) {
                res[1] = j;
                break;
            }
        }
        return res;
    }
}

36. 有效的数独 (opens new window)

class Solution {
    public boolean isValidSudoku(char[][] board) {
        // 行
        int[][] rows = new int [9][9];
        // 列
        int[][] columns = new int[9][9];
        // 九宫格
        int [][][] area = new int[3][3][9];
        
        // 第 i 行
        for (int i = 0; i < 9; i++) {
            // 第 j 列
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                // 如果当前位置不为空格，说明当前位置有数字
                if (c != '.') {
                    // 计算数字在数组中的索引（从0开始）
                    int index = c - '0' - 1;
                    // 将数字出现次数加1
                    rows[i][index]++;
                    columns[j][index]++;
                    area[i / 3][j / 3][index]++;
                    // 如果当前数字在当前行、当前列或当前九宫格中出现了2次以上，说明数独            不合法，直接返回false
                    if (rows[i][index] > 1 || columns[j][index] > 1 || area[i / 3][j / 3][index] > 1) {
                        return false;
                    }
                }
            }
        }
        return true;
    }
}

39. 组合总和 (opens new window)

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>(); // 定义结果列表
        if (len == 0) { // 如果候选数组为空，则直接返回空列表
            return res;
        }
        // 回溯 + 剪枝提速
        Arrays.sort(candidates); // 对候选数组进行排序，为后面的剪枝操作做准备
        Deque<Integer> path = new ArrayDeque<>(); // 定义双端队列，用于保存搜索路径
        dfs(candidates, 0, len, target, path, res); // 调用深度优先搜索方法
        return res; // 返回结果列表
    }
    // 深度优先搜索方法，接收候选数组、起始位置、数组长度、目标值、当前搜索路径和结果列表作为参数
    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况
        if (target == 0) { // 如果目标值等于 0，说明找到了一组解，将当前搜索路径添加到结果列表中
            res.add(new ArrayList<>(path));
            return; // 返回
        }
        // 遍历候选数组中从起始位置开始的所有元素
        for (int i = begin; i < len; i++) {
            // 如果当前元素比目标值大，则直接退出循环（剪枝操作）
            if (target - candidates[i] < 0) {
                break;
            }
            path.addLast(candidates[i]); // 将当前元素添加到搜索路径的末尾
            dfs(candidates, i, len, target - candidates[i], path, res); // 递归调用深度优先搜索方法
            path.removeLast(); // 将当前元素从搜索路径的末尾删除，继续遍历下一个元素
        }
    }
}

其中，path.removeLast(); 删除了哪个数?

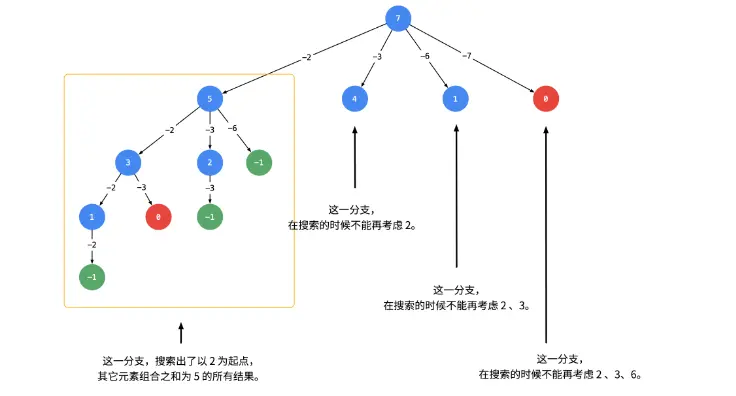
path.removeLast() 是将搜索路径 path 的末尾元素删除，也就是删除最后一个添加到路径中的元素，这个元素是上一个循环中添加到路径中的元素。可以理解为，每次进入下一层递归时，都会将当前元素添加到路径中，然后进行递归搜索；当递归返回时，需要将当前元素从路径中删除，回到上一层递归。因此，path.removeLast() 删除的是上一个递归中添加到路径中的元素。(比如 [2,2,3] 删除 3，一步步删)

树形图：

48. 旋转图像 (opens new window)

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地 (opens new window)** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

方法一：使用临时矩阵

    /**
     * 1、使用临时矩阵 -- 0ms(100.00%), 41.03MB(5.5%)
     * <p>
     * 时间复杂度：O(n ^ 2)
     * <p>
     * 空间复杂度：O(n ^ 2)
     */
    class Solution {
        public void rotate(int[][] matrix) {
            int n = matrix.length;
            // 创建一个临时矩阵
            int[][] temp = new int[n][];
            // 原矩阵深拷贝
            for (int i = 0; i < n; i++) {
                // 将原矩阵的值赋值给临时矩阵
                temp[i] = matrix[i].clone();
            }
            // 将临时矩阵的值赋值给原矩阵
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    matrix[j][n - 1 - i] = temp[i][j];
                }
            }
        }
    }

方法二：原地翻转

    /**
     * 2、原地翻转 -- 0ms(100.00%), 41.02MB(5.5%)
     * <p>
     * 时间复杂度：O(n ^ 2)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public void rotate(int[][] matrix) {
            int n = matrix.length;
            // 1、先对矩阵上下翻转（n >> 1 相当于 n / 2）
            for (int i = 0; i < n >> 1; i++) {
                for (int j = 0; j < n; j++) {
                    int temp = matrix[i][j];
                    matrix[i][j] = matrix[n - 1 - i][j];
                    matrix[n - 1 - i][j] = temp;
                }
            }
            // 2、然后对角线翻转
            for (int i = 0; i < n; i++) {
                // 注意：对角线翻转, j < i
                for (int j = 0; j < i; j++) {
                    int temp = matrix[i][j];
                    matrix[i][j] = matrix[j][i];
                    matrix[j][i] = temp;
                }
            }
        }
    }

49. 字母异位词分组 (opens new window)

问题描述

    /* 给你一个字符串数组，请你将 字母异位词 组合在一起。
       可以按任意顺序返回结果列表。
       字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 */

方法一：哈希表

    /**
     * 1、哈希表 -- 5ms(99.2%), 45.4MB(84.62%)
     * <p>
     * 时间复杂度：O(n * m * logm)
     * <p>
     * 空间复杂度：O(n * m)
     */
    class Solution {
        public List<List<String>> groupAnagrams(String[] strs) {
            Map<String, List<String>> map = new HashMap<>();

            for (String s : strs) {
                char[] t = s.toCharArray();
                Arrays.sort(t);
                String k = String.valueOf(t);

                // 1. 普通写法
                List<String> list = map.get(k);
                if (list == null) {
                    list = new ArrayList<>();
                    map.put(k, list);
                }
                list.add(s);

                // 2. Lambda表达式写法
                // map.computeIfAbsent(k, key -> new ArrayList<>())
                //         .add(s);

                // 3. 利用 map 内部方法：getOrDefault
                // List<String> list = map.getOrDefault(k, new ArrayList<String>());
                // list.add(s);
                // map.put(k, list);
            }

            return new ArrayList<>(map.values());
        }
    }

复杂度分析

n 是 String[] strs 中的字符串个数，m 是字符串数组中的字符串的最大长度

1、时间复杂度分析:

1. 排序部分的时间复杂度： 对每个字符串进行排序的时间复杂度是 O(m * log(m))。
2. 遍历部分的时间复杂度： 对 n 个字符串进行遍历，【每个】字符串在 map 中进行【操作】的时间复杂度是 O(1)。

所以，总的时间复杂度是排序部分的复杂度乘以遍历部分的复杂度，即 O(n * m * log(m))。

2、空间复杂度分析:

空间复杂度：O(n * m)，需要用哈希表存储全部字符串。