中等篇（下）
# 中等篇（下）
# 142. 环形链表 II (opens new window)
# 题目描述
简单来说，就是找到环的入口节点
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
1
2
3
2
3
示例 2：
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
1
2
3
2
3
示例 3：
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。
1
2
3
2
3
提示：
- 链表中节点的数目范围在范围
[0, 104]内 -105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引
**进阶：**你是否可以使用 O(1) 空间解决此题？
# 方法一：快慢指针
/**
* 1、快慢指针 -- 0ms(100.00%), 43.27MB(7.83%)
* <p>
* 时间复杂度：O(n)
* <p>
* 空间复杂度：O(1)
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
// 快慢指针，快指针每次移动两步，慢指针每次移动一步
ListNode fast = head, slow = head;
// 判断快慢指针是否相遇
while (fast != null && fast.next != null) {
// 慢指针每次移动一步
slow = slow.next;
// 快指针每次移动两步
fast = fast.next.next;
// 如果相遇，则表示有环
if (slow == fast) {
// 找到入环点
ListNode res = head;
// 判断入环点
while (res != slow) {
res = res.next;
slow = slow.next;
}
return res;
}
}
return null;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 算法图解
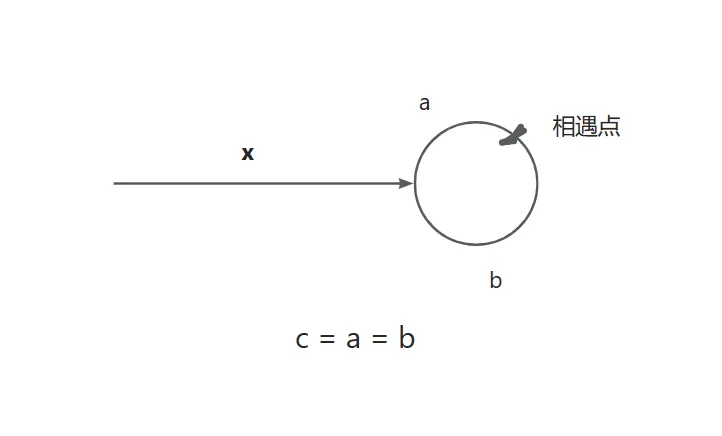
利用数学原理
假设
- x = 表头到环形入口点的距离
- a = 环形入口点到相遇点的距离
- b = 相遇点到环形入口点的距离
- c = a + b, 为环形的周长
- n = 快慢指针相遇时，快指针在环形中移动的圈数
则
- fast 指针移动了 2(x + a) 步
- slow 指针移动了 x + a + (n * c) 步
可得公式：
- 2(x + a) = x + a + (n * c)
- x + a = n * c
- x = n * c - (c - b)
- x = (n - 1) * c + b
- 由于 (n - 1) * c 代表圈数距离，所以可得 x = b
假设如下图所示：
这里简单画一下指针移动路线，不具体画出节点样式
# 146. LRU 缓存 (opens new window)
# 题目描述
请你设计并实现一个满足 LRU (最近最少使用) 缓存 (opens new window) 约束的数据结构。
实现 LRUCache 类：
LRUCache(int capacity)以 正整数 作为容量capacity初始化 LRU 缓存int get(int key)如果关键字key存在于缓存中，则返回关键字的值，否则返回-1。void put(int key, int value)如果关键字key已经存在，则变更其数据值value；如果不存在，则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity，则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例：
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
提示：
1 <= capacity <= 30000 <= key <= 100000 <= value <= 105- 最多调用
2 * 105次get和put
# 方法一：继承哈希链表
/**
* 1、继承哈希链表 -- 44ms(66.36%), 108.75MB(55.79%)
* <p>
* 时间复杂度：O(1)
* <p>
* 空间复杂度：O(capacity)
*/
class LRUCache extends LinkedHashMap<Integer, Integer> {
private int capacity;
public LRUCache(int capacity) {
super(capacity, 0.75F, true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key, -1);
}
// 这个可不写
public void put(int key, int value) {
super.put(key, value);
}
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 方法二：哈希表 + 双向链表
/**
* 2、哈希表 + 双向链表 -- 48ms(45.72%), 110.32MB(48.13%)
* <p>
* 时间复杂度：O(1)
* <p>
* 空间复杂度：O(capacity)
*/
class Node {
int key;
int val;
Node prev;
Node next;
Node() {
}
Node(int key, int val) {
this.key = key;
this.val = val;
}
}
class LRUCache2 {
private Map<Integer, Node> cache = new HashMap<>();
private Node head = new Node();
private Node tail = new Node();
private int capacity;
private int size;
public LRUCache2(int capacity) {
this.capacity = capacity;
head.next = tail;
tail.prev = head;
}
public int get(int key) {
if (!cache.containsKey(key)) {
return -1;
}
Node node = cache.get(key);
moveToHead(node);
return node.val;
}
public void put(int key, int value) {
if (cache.containsKey(key)) {
Node node = cache.get(key);
node.val = value;
moveToHead(node);
} else {
Node node = new Node(key, value);
cache.put(key, node);
addToHead(node);
++size;
if (size > capacity) {
node = removeTail();
cache.remove(node.key);
--size;
}
}
}
private void moveToHead(Node node) {
removeNode(node);
addToHead(node);
}
private void removeNode(Node node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void addToHead(Node node) {
node.next = head.next;
node.prev = head;
head.next = node;
node.next.prev = node;
}
private Node removeTail() {
Node node = tail.prev;
removeNode(node);
return node;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
# 148. 排序链表 (opens new window)
# 题目描述
给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。
示例 1：
输入：head = [4,2,1,3]
输出：[1,2,3,4]
1
2
2
示例 2：
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]
1
2
2
示例 3：
输入：head = []
输出：[]
1
2
2
提示：
- 链表中节点的数目在范围
[0, 5 * 104]内 -105 <= Node.val <= 105
**进阶：**你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？
# 方法一：自顶向下的归并排序
/**
* 1、自顶向下的归并排序 -- 11ms(59.03%), 55.63MB(18.42%)
* <p>
* 时间复杂度：O(nlogn)
* <p>
* 空间复杂度：O(n)
*/
public class Solution {
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
// 使用快慢指针找到中间节点
ListNode middle = findMiddle(head);
// 递归调用自己 -- 将链表分为两部分，分别排序
ListNode left = sortList(head);
ListNode right = sortList(middle);
// 合并两个有序链表
return merge(left, right);
}
private ListNode findMiddle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
ListNode middle = slow.next;
slow.next = null; // 断开链表，分为两部分
return middle;
}
private ListNode merge(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0);
ListNode current = dummy;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
current.next = l1;
l1 = l1.next;
} else {
current.next = l2;
l2 = l2.next;
}
current = current.next;
}
// 将未处理完的部分连接到已排序部分的末尾
if (l1 != null) {
current.next = l1;
} else {
current.next = l2;
}
return dummy.next;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# 方法二：自底向上的归并排序
/**
* 2、自底向上的归并排序 -- 16ms(22.15%), 55.25MB(31.37%)
* <p>
* 时间复杂度：O(nlogn)
* <p>
* 空间复杂度：O(1)
*/
public class Solution2 {
public ListNode sortList(ListNode head) {
// 如果链表为空或只有一个节点，无需排序，直接返回
if (head == null || head.next == null) {
return head;
}
// 获取链表的长度
int length = getLength(head);
// 创建一个虚拟节点作为辅助节点
ListNode dummy = new ListNode(0, head);
// 循环执行归并排序
for (int size = 1; size < length; size *= 2) {
ListNode prev = dummy;
ListNode curr = dummy.next;
// 分割、合并链表
while (curr != null) {
ListNode left = curr;
ListNode right = split(left, size);
curr = split(right, size);
prev = merge(left, right, prev);
}
}
return dummy.next;
}
// 获取链表的长度
private int getLength(ListNode head) {
int length = 0;
while (head != null) {
length++;
head = head.next;
}
return length;
}
// 将链表分为两部分，返回第二部分的头节点
private ListNode split(ListNode head, int size) {
if (head == null) {
return null;
}
for (int i = 1; i < size && head.next != null; i++) {
head = head.next;
}
ListNode second = head.next;
head.next = null;
return second;
}
// 合并两个已排序的链表，并连接到前一个节点
private ListNode merge(ListNode l1, ListNode l2, ListNode prev) {
ListNode curr = prev;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
curr.next = l1;
l1 = l1.next;
} else {
curr.next = l2;
l2 = l2.next;
}
curr = curr.next;
}
// 将剩余的部分连接到已排序的链表
curr.next = (l1 != null) ? l1 : l2;
// 移动到已排序链表的末尾
while (curr.next != null) {
curr = curr.next;
}
return curr;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
# 方法三：快速排序
/**
* 3、快速排序 -- 超出时间限制
* <p>
* 时间复杂度：最坏 -- O(n^2), 平均 -- O(nlogn)
* <p>
* 空间复杂度：最坏 -- O(n), 平均 -- O(logn)
*/
class Solution3 {
public ListNode sortList(ListNode head) {
return quickSortLinkedList(head)[0];
}
public ListNode[] quickSortLinkedList(ListNode head) {
if (head == null || head.next == null) return new ListNode[]{head, head};
// pivot为head，定义跟踪分割左右两个链表的头尾指针
ListNode p = head.next, headSmall = new ListNode(), headBig = new ListNode(), tailSmall = headSmall, tailBig = headBig;
// partition操作，以pivot为枢纽分割为两个链表
while (p != null) {
if (p.val < head.val) {
tailSmall.next = p;
tailSmall = tailSmall.next;
} else {
tailBig.next = p;
tailBig = tailBig.next;
}
p = p.next;
}
// 断开<pivot的排序链表、pivot、>=pivot的排序链表，链表变为三个部分
head.next = null;
tailSmall.next = null;
tailBig.next = null;
// 递归partition
ListNode[] left = quickSortLinkedList(headSmall.next);
ListNode[] right = quickSortLinkedList(headBig.next);
// 如果有<pivot的排序链表、连接pivot
if (left[1] != null) {
left[1].next = head;
}
// 连接pivot、>=pivot的排序链表
head.next = right[0];
// 确定排序后的头节点和尾节点
ListNode newHead, newTail;
if (left[0] != null) newHead = left[0];
else newHead = head;
if (right[1] != null) newTail = right[1];
else newTail = head;
// 返回当前层递归排序好的链表头节点和尾节点
return new ListNode[]{newHead, newTail};
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 方法四：动态数组
/**
* 4、动态数组 -- 12ms(45.77%), 53.89MB(75.78%)
* <p>
* 时间复杂度：O(nlogn)
* <p>
* 空间复杂度：O(n)
*/
class Solution4 {
public ListNode sortList(ListNode head) {
if (head == null) {
return null;
}
List<ListNode> list = new ArrayList<>();
while (head != null) {
list.add(head);
head = head.next;
}
list.sort(new Comparator<ListNode>() {
@Override
public int compare(ListNode o1, ListNode o2) {
return o1.val - o2.val;
}
});
for (int i = 0; i < list.size() - 1; i++) {
list.get(i).next = list.get(i + 1);
}
list.get(list.size() - 1).next = null;
return list.get(0);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 189. 轮转数组 (opens new window)
# 题目描述
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
1
2
3
4
5
6
2
3
4
5
6
示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
1
2
3
4
5
2
3
4
5
提示：
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
进阶：
- 尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。
- 你可以使用空间复杂度为
O(1)的 原地 算法解决这个问题吗？
# 方法一：复制数组
/**
* 1、复制数组 -- 1ms(63.85%), 55.85MB(5.03%)
* <p>
* 时间复杂度为：O(n)。
* <p>
* 空间复杂度为：O(n)。
*/
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
int[] newArr = new int[n];
for (int i = 0; i < n; i++) {
// if (i < k) {
// newArr[i] = nums[n - k + i];
// } else {
// newArr[i] = nums[i - k];
// }
newArr[(i + k) % n] = nums[i];
}
System.arraycopy(newArr, 0, nums, 0, n);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 方法二：三次翻转
/**
* 2、三次翻转 -- 0ms(100.00%), 56.47MB(5.03%)
* <p>
* 时间复杂度为：O(n)。
* <p>
* 空间复杂度为：O(1)。
*/
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
// 处理 k 大于数组长度的情况
k = k % n;
// 先翻转整个数组
reverse(nums, 0, n - 1);
// 再翻转前 k 个元素
reverse(nums, 0, k - 1);
// 最后翻转剩余的元素
reverse(nums, k, n - 1);
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 199. 二叉树的右视图 (opens new window)
# 题目描述
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
1
2
2
示例 2:
输入: [1,null,3]
输出: [1,3]
1
2
2
示例 3:
输入: []
输出: []
1
2
2
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
# 方法一：广度优先搜索
/**
* 1、广度优先搜索 -- 1ms(83.09%), 41.35MB(5.23%)
* <p>
* 时间复杂度：O(n)
* <p>
* 空间复杂度：O(n)
*/
class Solution {
public List<Integer> rightSideView(TreeNode root) {
// 如果根节点为空，返回一个空的整数列表
if (root == null) {
return new ArrayList<Integer>();
}
// 定义一个结果列表，用来存放右视图的节点值
List<Integer> result = new ArrayList<>();
// 定义一个队列，用来存储树的节点
Queue<TreeNode> queue = new LinkedList<>();
// 将根节点添加到队列中
queue.add(root);
// 当队列不为空时，进行循环
while (!queue.isEmpty()) {
// 获取队列的大小
int size = queue.size();
// 遍历队列中的节点
for (int i = 0; i < size; i++) {
// 从队列中取出当前节点
TreeNode currentNode = queue.poll();
// 如果当前节点是当前层的最后一个节点，将其值添加到结果列表中
if (i == size - 1) {
result.add(currentNode.val);
}
// 如果当前节点的左子节点不为空，将其添加到队列中
if (currentNode.left != null) {
queue.add(currentNode.left);
}
// 如果当前节点的右子节点不为空，将其添加到队列中
if (currentNode.right != null) {
queue.add(currentNode.right);
}
}
}
return result;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 方法二：深度优先搜索
/**
* 2、深度优先搜索 -- 0ms(100.00%), 41.14MB(15.11%)
* <p>
* 时间复杂度：O(n)
* <p>
* 空间复杂度：O(n)
*/
class Solution2 {
private List<Integer> res = new ArrayList<>();
public List<Integer> rightSideView(TreeNode root) {
dfs(root, 0);
return res;
}
private void dfs(TreeNode node, int depth) {
if (node == null) {
return;
}
if (depth == res.size()) {
res.add(node.val);
}
dfs(node.right, depth + 1);
dfs(node.left, depth + 1);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 230. 二叉搜索树中第K小的元素 (opens new window)
# 题目描述
给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。
示例 1：
输入：root = [3,1,4,null,2], k = 1
输出：1
1
2
2
示例 2：
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3
1
2
2
提示：
- 树中的节点数为
n。 1 <= k <= n <= 1040 <= Node.val <= 104
**进阶：**如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？
# 方法一：递归实现中序遍历（左根右）
/**
* 1、中序遍历（左根右） -- 0ms(100.00%), 43.52MB(6.72%)
* <p>
* 时间复杂度：O(n)
* <p>
* 空间复杂度：O(n)
*/
class Solution {
int res, k;
public int kthSmallest(TreeNode root, int k) {
this.k = k;
dfs(root);
return res;
}
void dfs(TreeNode root) {
if (root == null) {
return;
}
// 左 -- 根 -- 右
// 递归左子树
dfs(root.left);
// 返回当前节点的根节点值
if (k == 0) {
return;
}
// 返回当前节点值
if (--k == 0) {
res = root.val;
}
// 递归右子树
dfs(root.right);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 方法二：栈实现中序遍历
/**
* 2、中序遍历 -- 0ms(100.00%), 43.36MB(25.99%)
* <p>
* 时间复杂度：O(n)
* <p>
* 空间复杂度：O(n)
*/
class Solution {
public int kthSmallest(TreeNode root, int k) {
Stack<TreeNode> stk = new Stack<>();
while (root != null || !stk.isEmpty()) {
if (root != null) {
stk.push(root);
root = root.left;
} else {
root = stk.pop();
if (--k == 0) {
return root.val;
}
root = root.right;
}
}
return 0;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 236. 二叉树的最近公共祖先 (opens new window)
# 题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科 (opens new window)中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
示例 1：
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
1
2
3
2
3
# 方法一：DFS 递归
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 终止条件：如果当前节点为空，或者当前节点是p或q中的一个，则直接返回当前节点
if (root == null || root == p || root == q) {
return root;
}
// 递归左子树：递归查找左子树中是否存在p或q的公共祖先
var left = lowestCommonAncestor(root.left, p, q);
// 递归右子树：递归查找右子树中是否存在p或q的公共祖先
var right = lowestCommonAncestor(root.right, p, q);
// 如果左右子树都找到了非空结果，说明当前节点就是它们的公共祖先
if (left != null && right != null) {
return root;
}
// 如果只有其中一个子树返回了非空结果，则说明p和q都在该子树中，返回对应的子树结果
// 如果两边都是null，则返回null表示没有找到公共祖先节点
return left == null ? right : left;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
算法图解：
- https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/solutions/240096/236-er-cha-shu-de-zui-jin-gong-gong-zu-xian-hou-xu
# 238. 除自身以外数组的乘积 (opens new window)
# 题目描述
给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 **不要使用除法，**且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
1
2
2
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
1
2
2
提示：
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
**进阶：**你可以在 O(1) 的额外空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组 不被视为 额外空间。）
# 方法一：两次循环
/**
* 1、两次循环 -- 1ms(100.00%), 51.84MB(9.51%)
* <p>
* 时间复杂度为：O(n)。
* <p>
* 空间复杂度为：O(1), 忽略答案数组的空间消耗，额外空间复杂度为 O(1)。
*/
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] ans = new int[n];
// 计算每个元素的前缀积（即下三角）
for (int i = 0, down = 1; i < n; i++) {
ans[i] = down;
down *= nums[i];
}
// 计算每个元素的后缀积（即上三角）
for (int i = n - 1, up = 1; i >= 0; i--) {
ans[i] *= up;
up *= nums[i];
}
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 240. 搜索二维矩阵 II (opens new window)
# 题目描述
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1：
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
1
2
2
示例 2：
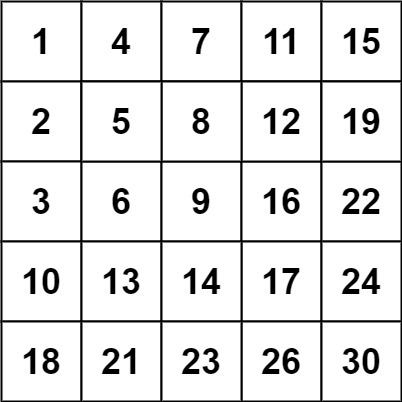
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false
1
2
2
提示：
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
# 方法一：二分查找
二分查找每一行的元素：
/**
* 1、二分查找 -- 6ms(47.09%), 45.01MB(96.77%)
* <p>
* 时间复杂度：O(mlogn), 其中 m 和 n 分别为矩阵的行数和列数。
* <p>
* 空间复杂度：O(1)
*/
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
// 遍历矩阵中的每一行，使用二分查找法查找target是否存在
for (int[] row : matrix) {
// 返回的 b 代表在数组 row 中查找元素 target 的位置, 即索引值
int b = Arrays.binarySearch(row, target);
if (b >= 0) {
return true;
}
}
return false;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 方法二：贪心（左下角开始搜索）
以下代码题解，是从左下角往右上方向开始搜索，比较当前元素 matrix[i][j]与 target 的大小关系：
/**
* 2、贪心：从左下角或右上角搜索 -- 6ms(47.09%), 45.06MB(96.30%)
* <p>
* 时间复杂度：O(m + n), 其中 m 和 n 分别为矩阵的行数和列数。
* <p>
* 空间复杂度：O(1)
*/
class Solution2 {
public boolean searchMatrix(int[][] matrix, int target) {
// 获取矩阵的行数和列数
int m = matrix.length, n = matrix[0].length;
// 初始化行索引和列索引（左下角）
int i = m - 1, j = 0;
// 当行索引大于等于0 且 列索引小于列数时，进行循环
while (i >= 0 && j < n) {
// 如果当前元素等于目标值，返回true
if (matrix[i][j] == target) {
return true;
}
// 如果当前元素大于目标值，将行索引减1
if (matrix[i][j] > target) {
--i;
} else {
// 如果当前元素小于目标值，将列索引加1
++j;
}
}
// 如果循环结束后仍未找到目标值，返回false
return false;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
解析：
这段代码是贪心算法的一种实现，具体体现在从左下角或右上角搜索目标值。在循环中，根据当前元素与目标值的大小关系，更新行索引或列索引，从而逐步缩小搜索范围。当找到目标值时，返回 true；如果循环结束后仍未找到目标值，则返回 false。
# 437. 路径总和 III (opens new window)
# 题目描述
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。
示例 1：
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
1
2
3
2
3
示例 2：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3
1
2
2
# 方法一：哈希表 + 前缀和 + 递归
class Solution {
// 用于记录前缀和出现的次数
private Map<Long, Integer> cnt = new HashMap<>();
// 目标路径和
private int targetSum;
public int pathSum(TreeNode root, int targetSum) {
// 初始化前缀和映射，0 出现了一次（空路径）
cnt.put(0L, 1);
this.targetSum = targetSum;
return dfs(root, 0);
}
private int dfs(TreeNode node, long s) {
if (node == null) {
return 0;
}
// 当前路径和
s += node.val;
// 检查是否存在满足条件的路径：当前前缀和减去目标值已被记录
int ans = cnt.getOrDefault(s - targetSum, 0);
// 将当前前缀和加入映射表（1：要增加的计数值。Integer::sum：合并函数，用于当键已存在时将旧值与新值相加。）
cnt.merge(s, 1, Integer::sum);
// 向左右子节点递归探索
ans += dfs(node.left, s);
ans += dfs(node.right, s);
// 回溯，将当前前缀和从映射表中移除
cnt.merge(s, -1, Integer::sum);
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 438. 找到字符串中所有字母异位词 (opens new window)
# 题目描述
给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。
示例 1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
1
2
3
4
5
2
3
4
5
示例 2:
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
1
2
3
4
5
6
2
3
4
5
6
# 方法一：滑动窗口（双指针+哈希表）
/**
* 1、滑动窗口（双指针+哈希表） -- 38ms(26.77%), 42.73MB(62.58%)
* <p>
* 时间复杂度为 O(p + s), p 是字符串 p 的长度, s是字符串 s 的长度
* <p>
* 空间复杂度为 O(p), p 是字符串 p 的长度
*/
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> result = new ArrayList<>();
// 存储目标字符串 p 中每个字符的出现次数
HashMap<Character, Integer> targetFreqMap = new HashMap<>();
for (char c : p.toCharArray()) {
targetFreqMap.put(c, targetFreqMap.getOrDefault(c, 0) + 1);
}
int pLen = p.length();
int left = 0, right = 0, count = pLen;
while (right < s.length()) {
char currentChar = s.charAt(right);
// 如果当前字符是目标字符串 p 中的字符，更新 count
if (targetFreqMap.containsKey(currentChar) && targetFreqMap.get(currentChar) > 0) {
count--;
}
// 更新目标字符串中当前字符的出现次数
targetFreqMap.put(currentChar, targetFreqMap.getOrDefault(currentChar, 0) - 1);
// 移动右指针
right++;
// 当 count 等于 0 时，表示找到一个合法的字母异位词
if (count == 0) {
result.add(left);
}
// 当窗口大小等于目标字符串长度时，左指针右移，恢复 count 和频率表
if (right - left == pLen) {
char leftChar = s.charAt(left);
// 恢复 count
if (targetFreqMap.containsKey(leftChar) && targetFreqMap.get(leftChar) >= 0) {
count++;
}
// 恢复频率表
targetFreqMap.put(leftChar, targetFreqMap.getOrDefault(leftChar, 0) + 1);
// 移动左指针
left++;
}
}
return result;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# 代码解析
这个解法使用了滑动窗口的思想，通过维护一个窗口，在窗口内判断是否为字母异位词。
下面是该解法的逻辑解释：
- 初始化： 首先，构建目标字符串
p的字符频率表targetFreqMap，用于存储每个字符在目标字符串中的出现次数。 - 滑动窗口： 使用两个指针
left和right维护一个窗口，表示当前处理的子字符串。初始化时，窗口大小为目标字符串p的长度。还有一个计数器count，表示当前窗口中还需要找到的字符的数量。 - 移动右指针： 逐步右移
right指针，更新窗口内字符的频率信息。对于每个右移的字符，检查它是否在目标字符串p的频率表中，并且它的频率是否大于 0。如果是，将count减一，表示找到了一个符合条件的字符。 - 找到异位词： 当
count等于 0 时，表示当前窗口内的字符与目标字符串p中的字符构成了一个字母异位词，将当前左指针left的位置加入结果列表。 - 移动左指针： 当窗口大小等于目标字符串长度时，左指针右移。在右移之前，检查离开窗口的字符，如果它是目标字符串中的字符，将
count恢复，并更新频率表。 - 重复过程： 重复上述过程，直到右指针
right移动到字符串s的末尾。
通过这种方式，可以有效地在字符串 s 中找到所有与目标字符串 p 是字母异位词的子串的起始位置。这个算法的时间复杂度为 O(p + s)，其中 p 是字符串 p 的长度，s 是字符串 s 的长度。空间复杂度为 O(p)。
# 方法二：滑动窗口优化版（双指针+数组）
/**
* 2、滑动窗口优化版（双指针+数组） -- 4ms(98.83%), 42.32MB(97.00%)
* <p>
* 时间复杂度为 O(m + n), m 是字符串 s 的长度, n 是字符串 p 的长度
* <p>
* 空间复杂度为 O(C), C 是字符集大小, 即 C = 26
*/
class Solution {
public List<Integer> findAnagrams(String s, String p) {
// 计算s和p的长度
int m = s.length(), n = p.length();
// 创建一个存储结果的列表
List<Integer> res = new ArrayList<>();
// 如果s的长度小于p的长度，则直接返回空列表
if (m < n) {
return res;
}
// 创建一个长度为26的数组，用来存储p中每个字符出现的次数
int[] cnt1 = new int[26];
// 遍历p，将每个字符出现的次数存入cnt1中
for (int i = 0; i < n; ++i) {
cnt1[p.charAt(i) - 'a']++;
}
// 创建一个长度为26的数组，用来存储s中每个字符出现的次数
int[] cnt2 = new int[26];
// 遍历s，将每个字符出现的次数存入cnt2中
for (int i = 0, j = 0; i < m; ++i) {
int k = s.charAt(i) - 'a';
cnt2[k]++;
// 如果cnt2中某个字符出现的次数大于cnt1中对应字符出现的次数，则将cnt2中对应字符出现的次数减1，并且j自增1
while (cnt2[k] > cnt1[k]) {
cnt2[s.charAt(j++) - 'a']--;
}
// 如果i - j + 1等于n，则将j的值存入res中
if (i - j + 1 == n) {
res.add(j);
}
}
// 返回res
return res;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 代码解析
这个解法同样使用了滑动窗口的思想，不同之处在于优化了空间复杂度，使用了长度为 26 的数组 cnt1 和 cnt2 代替哈希表，用来存储字符的频率信息。
下面是该解法的逻辑解释：
- 初始化： 创建两个长度为 26 的数组
cnt1和cnt2，用来分别存储字符串p和字符串s中每个字符的频率信息。 - 遍历字符串 p： 遍历字符串
p，将每个字符出现的次数存入cnt1中。 - 遍历字符串 s： 在遍历字符串
s的同时，维护一个窗口，通过更新cnt2数组来表示窗口中字符的频率。 - 滑动窗口：
- 对于每个右移的字符，将
cnt2中对应字符的频率加一。 - 如果某个字符的频率在
cnt2中超过了cnt1中对应字符的频率，说明这个字符在当前窗口中出现次数过多，需要左移窗口的左边界，即增大j。 - 左移窗口的同时，更新
cnt2中左边界字符的频率。 - 如果窗口大小等于字符串
p的长度，说明找到了一个字母异位词，将窗口的左边界j存入结果列表。
- 对于每个右移的字符，将
- 返回结果： 返回存储结果的列表。
通过这种方式，代码实现了在字符串 s 中找到所有与目标字符串 p 是字母异位词的子串的起始位置。这个算法的时间复杂度为 O(m + n)，其中 m 是字符串 s 的长度，n 是字符串 p 的长度。空间复杂度为 O(26)，即 O(1)，因为字符集的大小是固定的。
# 560. 和为 K 的子数组 (opens new window)
# 题目描述
给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1：
输入：nums = [1,1,1], k = 2
输出：2
1
2
2
示例 2：
输入：nums = [1,2,3], k = 3
输出：2
1
2
2
# 方法一：暴力解法
/**
* 1、暴力解法 -- 1606ms(31.36%), 44.44MB(53.38%)
* <p>
* 时间复杂度分析：O(n^2)，其中 n 是数组的长度。
* <p>
* 空间复杂度分析：O(1)。
*/
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0;
int len = nums.length;
for (int left = 0; left < len; left++) {
int sum = 0;
for (int right = left; right < len; right++) {
sum += nums[right];
if (sum == k) {
count++;
}
}
}
return count;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 方法二：前缀和 + 哈希表
/**
* 2、前缀和 + 哈希表 -- 25ms(54.20%), 46.03MB(5.03%)
* <p>
* 时间复杂度：O(n)。
* <p>
* 空间复杂度为：O(n)。
*/
class Solution {
public int subarraySum(int[] nums, int k) {
// 创建一个哈希表，用于存储前缀和及其出现的次数
Map<Integer, Integer> counter = new HashMap<>();
// 初始化哈希表，表示前缀和为 0 出现了 1 次
counter.put(0, 1);
// 初始化答案为 0，s 用于表示当前的前缀和
int ans = 0, s = 0;
// 遍历数组 nums 中的每个元素
for (int num : nums) {
// 计算当前的前缀和
s += num;
// 更新答案，如果存在前缀和为 (s - k) 的情况，累加对应次数到答案中
ans += counter.getOrDefault(s - k, 0);
// 更新哈希表，记录当前前缀和出现的次数
counter.put(s, counter.getOrDefault(s, 0) + 1);
}
// 返回最终答案
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 代码分析
- 这个算法的关键思想是通过维护前缀和的累加和哈希表，记录前缀和出现的次数。
- 在遍历数组时，对于当前前缀和
s，如果存在s - k出现过，那么就说明在这之前有子数组的和为k，累加对应的次数到答案中。 - 最后，更新哈希表，记录当前前缀和的次数。
# 什么是前缀和？
前缀和与子数组的个数之间存在着紧密的关系，尤其在解决子数组和相关问题时。
前缀和是指从数组起始位置开始，到数组中某个位置的所有元素之和。
以下是关于前缀和和子数组个数之间的关系的解释：
- 前缀和数组： 给定数组
nums，可以计算前缀和数组prefixSum，其中prefixSum[i]表示数组前i个元素的和。形式化地，prefixSum[i] = nums[0] + nums[1] + ... + nums[i-1]。 - 子数组和： 对于数组
nums中的任意子数组[i, j]，其和可以通过前缀和数组计算得到。子数组和为nums[i] + nums[i+1] + ... + nums[j]，可以表示为prefixSum[j+1] - prefixSum[i]。 - 计算子数组和为 K 的个数： 对于给定的整数 K，我们可以通过计算前缀和数组来确定子数组和为 K 的个数。假设
s是当前的前缀和，那么我们只需要查找之前是否存在前缀和s - K，如果存在，说明从那个位置到当前位置的子数组和为 K。- 如果存在
counter[s - K]，则累加counter[s - K]到答案中，表示有counter[s - K]个子数组的和为 K。 - 更新哈希表，将当前前缀和
s的次数加一，表示我们已经经过了当前位置。
- 如果存在
- 计算子数组和为 K 的个数的应用：
- 最大子数组和： 通过计算每个位置的前缀和，可以在 O(n) 的时间复杂度内找到数组中的最大子数组和。
- 和为 K 的子数组： 通过维护前缀和和哈希表，在 O(n) 的时间内找到数组中和为 K 的子数组的个数。
- 连续子数组的最大/最小值： 通过前缀和和一些额外的处理，可以在 O(n) 的时间内找到连续子数组的最大/最小值。
为什么对于当前前缀和
s，如果存在s - k出现过，那么就说明在这之前有子数组的和为k?
假设 s 是当前的前缀和，s - k 表示从数组开始的某个位置（在当前位置之前）到当前位置的子数组的和。
如果我们找到了某个位置 i，使得 prefixSum[i] = s - k，那么说明从 i 位置到当前位置的子数组和为 k。
上次更新: 2025/5/20 17:42:11