计算机基础
数据结构与算法
基础篇

栈

# 栈

# 简介

栈是一种特殊的线性表，只能在一端进行操作

往栈中添加元素的操作，一般叫做 push，入栈
从栈中移除元素的操作，一般叫做 pop，出栈(只能移除栈顶元素，也叫做: 弹出栈顶元素)
后进先出的原则，Last In First Out，LIFO

# 接口设计

一般设计以下几种接口，添加删除操作都是 O(1) 级别

返回栈底元素：top() 相当于官方的 peek()

# 代码实现

内部实现可利用到之前学习的数据结构：动态数组，链表

public class Stack<E> {
  
	private List<E> list = new ArrayList<>();
	
	public void clear() {
		list.clear();
	}
	
	public int size() {
		return list.size();
	}

	public boolean isEmpty() {
		return list.isEmpty();
	}

	public void push(E element) {
		list.add(element); // 相当于在数组尾部添加元素
	}

	public E pop() {
		return list.remove(list.size() - 1); // 相当于在数组尾部删除元素，并返回被删除的元素
	}

	public E top() {
		return list.get(list.size() - 1);
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

接口测试

public class Main {

	public static void main(String[] args) {
		Stack<Integer> stack = new Stack<>();
		stack.push(11);
		stack.push(22);
		stack.push(33);
		stack.push(44);

		while (!stack.isEmpty()) {
			System.out.println(stack.pop());
		}
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

可查看官方实现

java.util.Stack<Integer> stack;

# 栈的应用举例

1、浏览器的前进和后退（应用到两个栈）

2、软件的撤销（Undo）、恢复（Redo）功能

具体解析

后退：

后退操作：第一个栈的栈顶元素被弹出（pop），进入第二个栈（push）

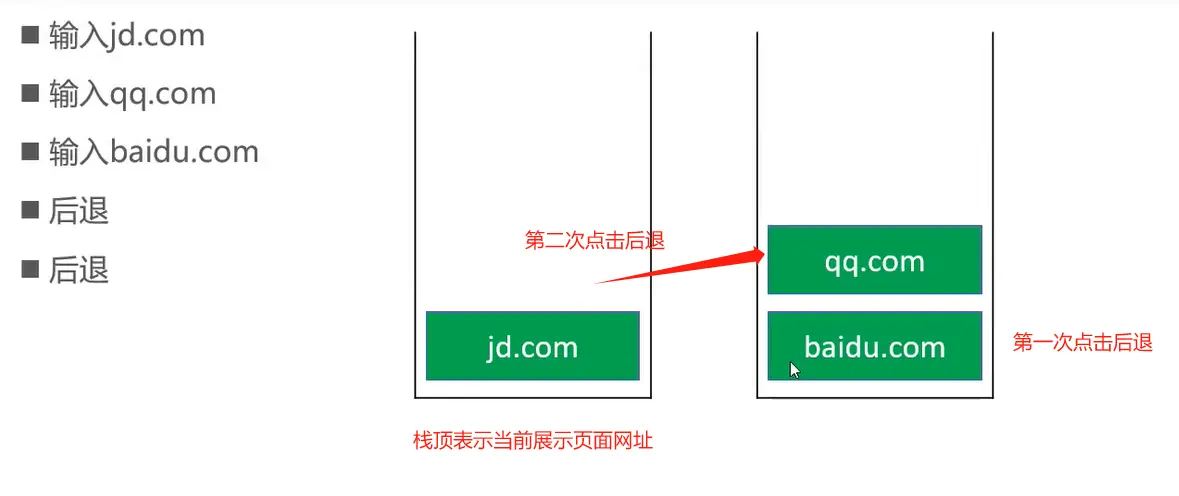
前进：

前进操作：第二个栈的元素被弹出（pop），进入第一个栈（push）

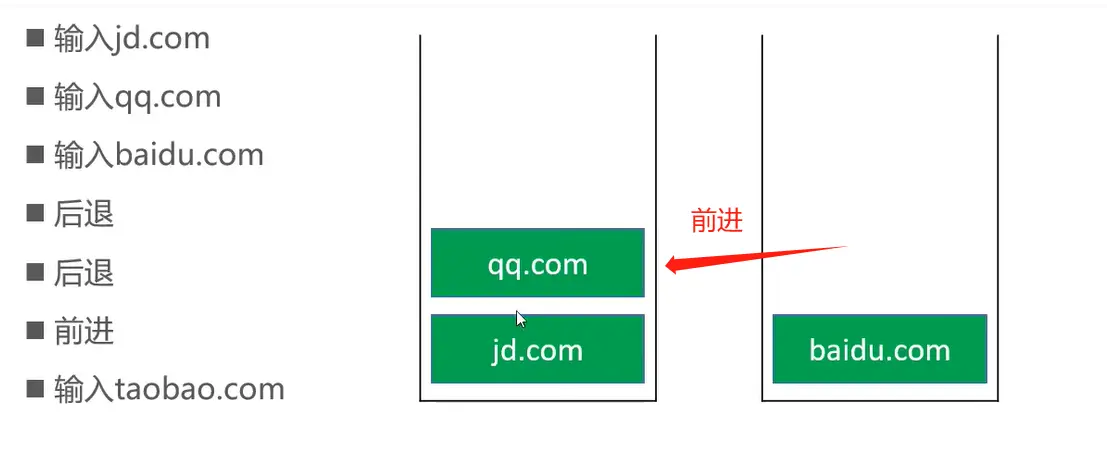
输入新网址：

新网址进入第一个栈（push），第二个栈保存的元素被清空（clear）

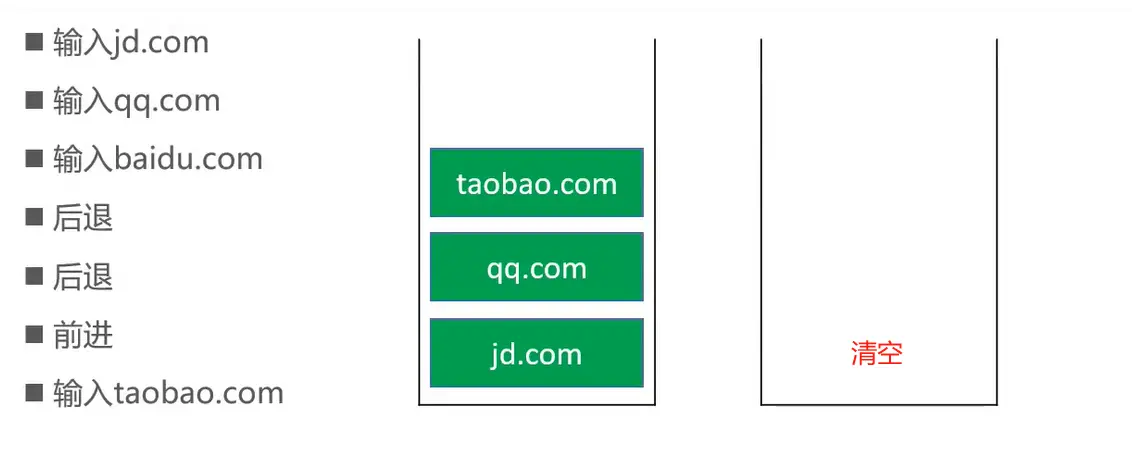
# 练习

# 20.有效的括号

官方地址：20. 有效的括号 - 力扣（LeetCode） (opens new window)

# 解法一

用 空字符串替换 的方法

class Solution {
    public boolean isValid(String s) {

        while(s.contains("()") || s.contains("{}") || s.contains("[]")) {
            s = s.replace("()", "");
            s = s.replace("{}", "");
            s = s.replace("[]", "");
        }
        return s.isEmpty();

    }
}

1
2
3
4
5
6
7
8
9
10
11
12

缺点：

效率非常低，耗内存。

原因：

字符串的查找操作跟字符串的替换操作都是非常耗性能的，而且字符串是不可变的。字符串不可变，它就会不断地去产生新的字符串，这样会浪费内存，而且效率特别低。

# 解法二

用栈方法

class Solution {
    public boolean isValid(String s) {

        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c == '(' || c == '{' || c == '[') { // 左括号
                stack.push(c); // 入栈
            } else { // 右括号
                if (stack.isEmpty()) return false;

                char left = stack.pop(); // 出栈
                if (left == '(' && c != ')') return false;
                if (left == '{' && c != '}') return false;
                if (left == '[' && c != ']') return false;

            }
        }
        return stack.isEmpty();

    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 解法三

用 Map（字典）+ 栈 的方法。

class Solution {

    private static final HashMap<Character, Character> map = new HashMap<>();
    static {
        map.put('(',')');
        map.put('{','}');
        map.put('[',']');
    }

    public boolean isValid(String s) {

        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (map.containsKey(c)) {
                stack.push(c);
            } else {
                if (stack.isEmpty()) return false;

                char left = stack.pop();
                if (c != map.get(left)) return false;
            }
        }
        return stack.isEmpty();

    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 856.括号的方数

官方地址：856. 括号的分数 - 力扣（LeetCode） (opens new window)

# 36.逆波兰表达式求值

官方地址：LCR 036. 逆波兰表达式求值 - 力扣（LeetCode） (opens new window)

# 224.基本计算器

官方地址：224. 基本计算器 - 力扣（LeetCode） (opens new window)

上次更新: 2024/9/25 11:16:13

← 链表队列→