沉梦听雨的编程指南
  • 计算机基础
  • 数据结构与算法
  • 基础篇
沉梦听雨
2023-08-25
目录

复杂度

# 复杂度

# 什么是算法？

算法是用于解决特定问题的一系列的执行步骤。

比如计算 a + b 的和以及 1 到 n 的和。

# 斐波那契数

使用不同的算法，解决同一个问题，效率可能相差非常大

  • 比如：求第 n 个斐波那契数(fibonacci number)

代码如下：

	/* 0 1 2 3 4 5
	 * 0 1 1 2 3 5 8 13 ....
	 */
	
	// O(2^n)
	public static int fib1(int n) {
		if (n <= 1) return n;
		return fib1(n - 1) + fib1(n - 2);
	}
	
	// O(n)
	public static int fib2(int n) {
		if (n <= 1) return n;
		
		int first = 0;
		int second = 1;
		for (int i = 0; i < n - 1; i++) {
			int sum = first + second;
			first = second;
			second = sum;
		}
		return second;
	}

	public static void main(String[] args) {
		int n = 46;
		
		TimeTool.check("fib1", new Task() {
			public void execute() {
				System.out.println(fib1(n));
			}
		});
		
		TimeTool.check("fib2", new Task() {
			public void execute() {
				System.out.println(fib2(n));
			}
		});
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

性能对比：fib2 > fib1

时间工具类

public class TimeTool {
	private static final SimpleDateFormat fmt = new SimpleDateFormat("HH:mm:ss.SSS");
	
	public interface Task {
		void execute();
	}
	
	public static void check(String title, Task task) {
		if (task == null) return;
		title = (title == null) ? "" : ("【" + title + "】");
		System.out.println(title);
		System.out.println("开始：" + fmt.format(new Date()));
		long begin = System.currentTimeMillis();
		task.execute();
		long end = System.currentTimeMillis();
		System.out.println("结束：" + fmt.format(new Date()));
		double delta = (end - begin) / 1000.0;
		System.out.println("耗时：" + delta + "秒");
		System.out.println("-------------------------------------");
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 如何评判一个算法的好坏？

# 事后统计法

如果单从执行效率上进行评估，可能会想到这么一种方案 -- 事后统计法

也就是：比较不同算法对同一组输入的执行处理时间

不过上述方案有比较明显的缺点

  • 执行时间严重依赖硬件以及运行时各种不确定的环境因素
  • 必须编写相应的测算代码
  • 测试数据的选择比较难保证公正性

# 复杂度分析

一般从以下维度来评估算法的优劣

  • 正确性、可读性、健壮性 (对不合理输入的反应能力和处理能力)
  • 时间复杂度 (time complexity) : 估算程序指的执行次数 (执行时间)
  • 空间复杂度(space complexity) : 估算所需占用的存储空间

# 时间复杂度估算

# 大 O 表示法（Big O)

一般用大 O 表示法来描述复杂度，它表示的是数据规模 n 对应的复杂度

  • 忽略常数、系数、低阶
  • 9 >> O(1)
  • 2n+3 >> O(n)
  • n^2 + 2n +6 >> O(n^2)
  • 4n^3 + 3n^2 + 22n + 100 >> O(n^3)
  • 写法上，n 的 3 次方等价于 n^3

注意：大 O 表示法仅仅是一种粗略的分析模型，是一种估算，能帮助我们短时间内了解一个算法的执行效率

# 执行次数的计算

先看下代码的执行次数是如何计算的

public static void test1(int n) {
  
		// 1
		if (n > 10) { 
			System.out.println("n > 10");
		} else if (n > 5) { // 2
			System.out.println("n > 5");
		} else {
			System.out.println("n <= 5"); 
		}
		
		// 1 + 4 + 4 + 4
		for (int i = 0; i < 4; i++) {
			System.out.println("test");
		}
		
		// 执行次数：14
    // 渐进时间复杂度 O(1)
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

为什么执行次数是 14

  1. if 判断里面执行只有 1 次
  2. for 循环里面。
    • int i = 0 执行一次
    • i < 4 执行 4 次
    • i++ 执行 4 次
    • 代码块的语句执行 4 次
    • 一共是 1 + 4 + 4 + 4 = 13 次
  3. 所以这个方法的总共执行次数是 1 + 13 = 14 次，用大 O 表示法为 O（1）

以下是其他一些示例

	public static void test2(int n) {
		// O(n)
		// 1 + 3n
		for (int i = 0; i < n; i++) {
			System.out.println("test");
		}
	}

	public static void test3(int n) {
		// 1 + 2n + n * (1 + 3n)
		// 1 + 2n + n + 3n^2
		// 3n^2 + 3n + 1
		// O(n^2)

		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				System.out.println("test");
			}
		}
	}

	public static void test4(int n) {
		// 1 + 2n + n * (1 + 45)
		// 1 + 2n + 46n
		// 48n + 1
		// O(n)
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < 15; j++) {
				System.out.println("test");
			}
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 对数阶的细节

对数阶一般省略底数

比如： $$ log2(n) = log2(9) * log9(n) $$ 所以 log2(n)、log9(n) 统称为 log(n)

代码示例如下：

	public static void test5(int n) {
		// 8 = 2^3
		// 16 = 2^4
		
		// 3 = log2(8)
		// 4 = log2(16)
		
		// 执行次数 = log2(n)
		// O(logn)
		while ((n = n / 2) > 0) {
			System.out.println("test");
		}
	}

	public static void test6(int n) {
		// log5(n)
		// O(logn)
		while ((n = n / 5) > 0) {
			System.out.println("test");
		}
	}

	public static void test7(int n) {
		// 1 + 2*log2(n) + log2(n) * (1 + 3n)
		
		// 1 + 3*log2(n) + 2 * nlog2(n)
		// O(nlogn)
		for (int i = 1; i < n; i = i * 2) {
			// 1 + 3n
			for (int j = 0; j < n; j++) {
				System.out.println("test");
			}
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 常见复杂度

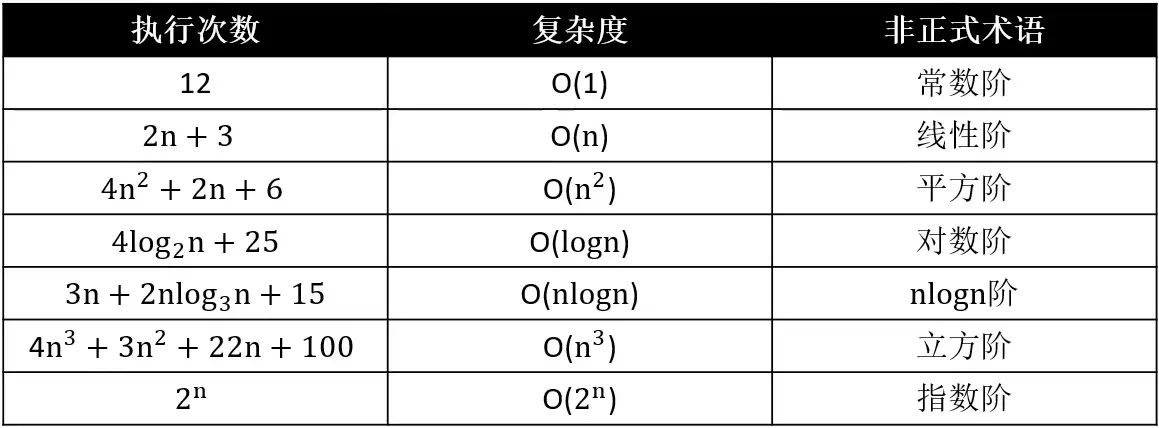
image

耗时比较

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

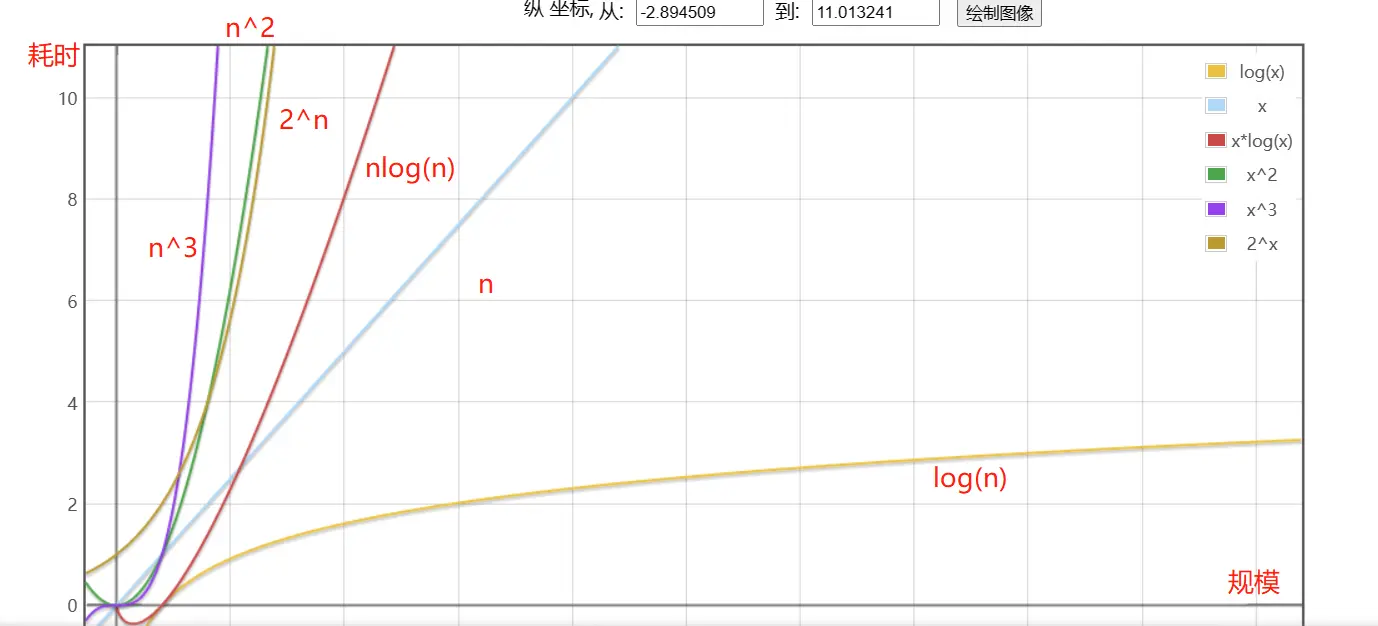
# 对比复杂度大小的工具

函数图像绘制工具 (numberempire.com) (opens new window)

规模较小时

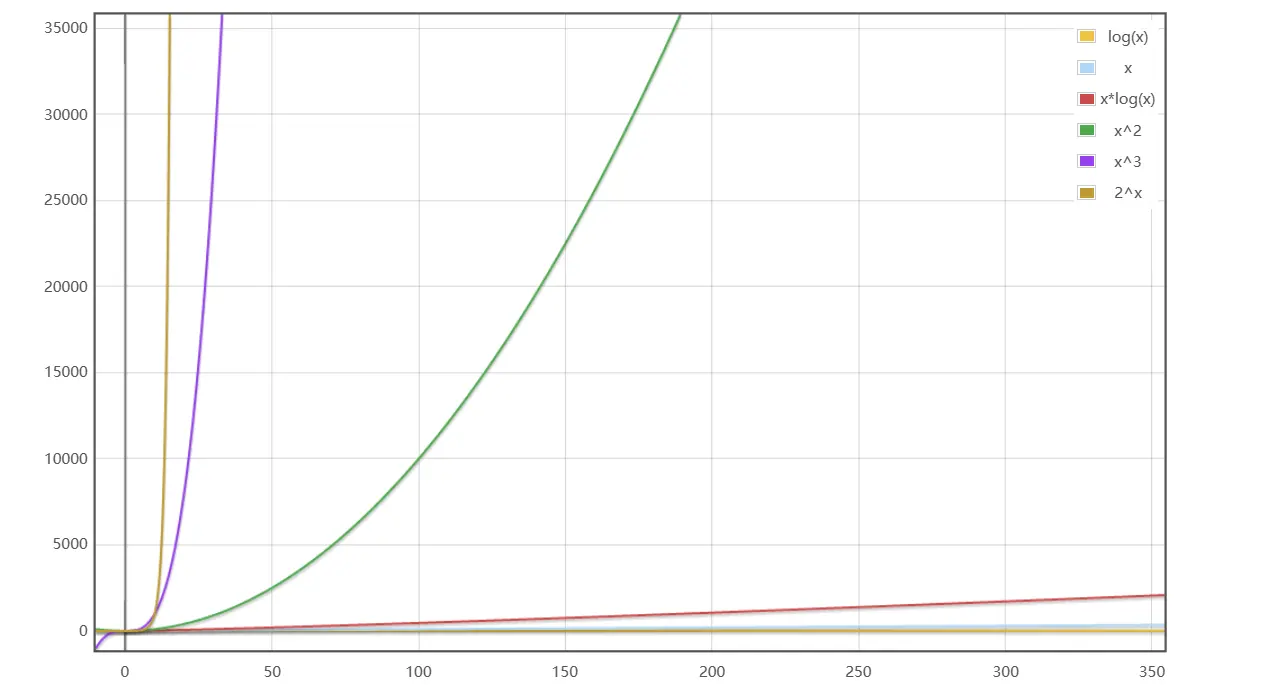
image

规模较大时

image

# 空间复杂度估算

空间复杂度: 估算所需占用的存储空间。

代码分析：

public static void test1(int n) {

		if (n > 10) { 
			System.out.println("n > 10");
		} else if (n > 5) { // 2
			System.out.println("n > 5");
		} else {
			System.out.println("n <= 5"); 
		}

		for (int i = 0; i < 4; i++) {
			System.out.println("test");
		}

    // 空间复杂度 O(1)
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

因为只定义了一个 int i = 0，所以空间复杂度为 O(1)

再分析下这个代码：

	public static void test10(int n) {
		// O(n)
		int a = 10;
		int b = 20;
		int c = a + b;
		int[] array = new int[n];
		for (int i = 0; i < array.length; i++) {
			System.out.println(array[i] + c);
		}
	}
1
2
3
4
5
6
7
8
9
10

空间复杂度为 O(n), 因为 int n, new int[n] 定义了数组空间为 n 个，常数项的空间复杂度忽略不计。

# 斐波那契数复杂度分析

1、先分析下 fib1 方法

	/* 0 1 2 3 4 5
	 * 0 1 1 2 3 5 8 13 ....
	 */
	
	// O(2^n)
	public static int fib1(int n) { // 递归
		if (n <= 1) return n;
		return fib1(n - 1) + fib1(n - 2);
	}
1
2
3
4
5
6
7
8
9

fib(n) 执行了多少次，时间复杂度就是多少。

接下来分析一下 fib(5) 这个函数

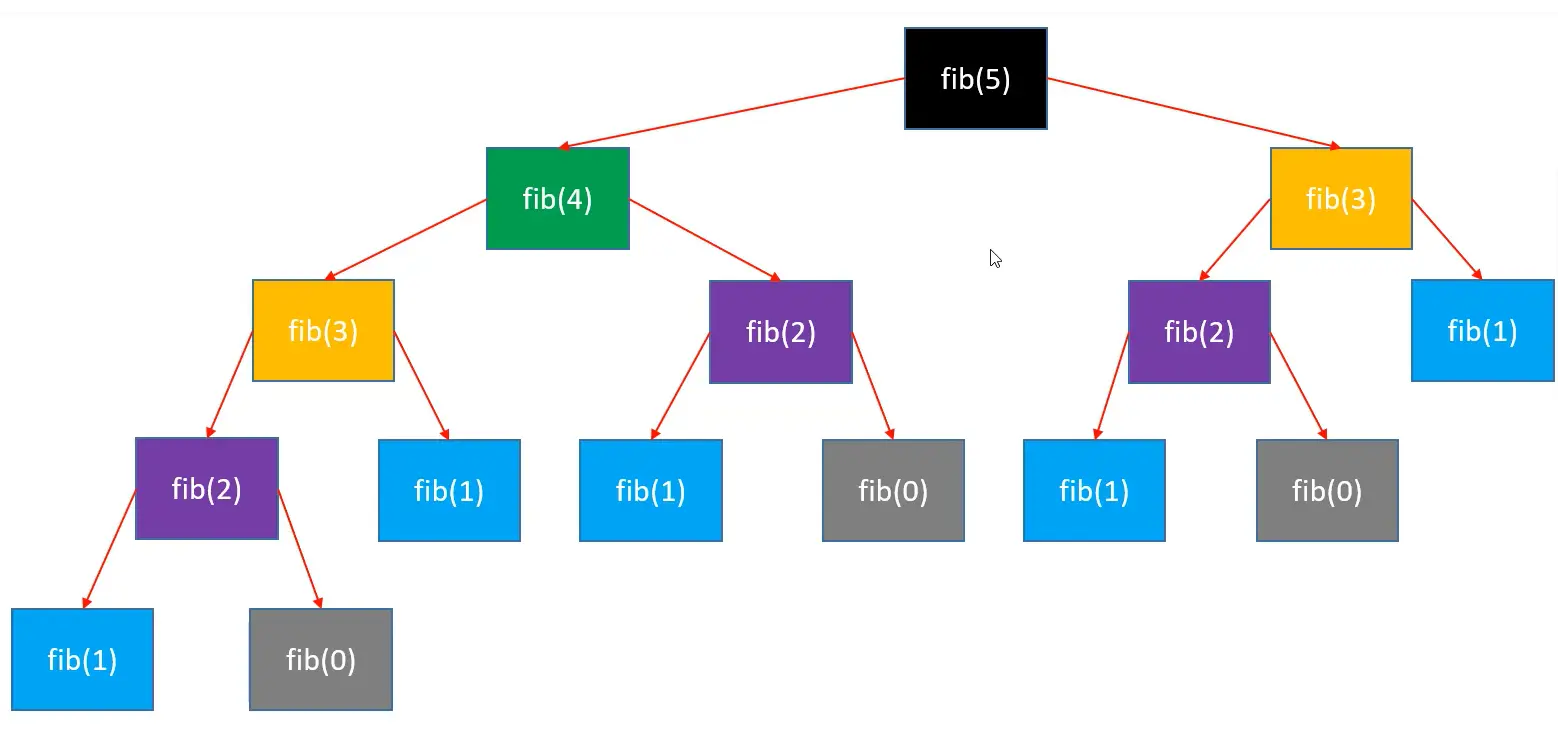
image

  • 总共执行次数 = 1 + 2 + 4 + 8 = 2^0 + 2^1 + 2^2 + 2^3 = 2^4 -1 = 2^(n-1) - 1 = 0.5 * 2^n - 1（这里并不是说 fib(6) 就符合这条格式）
  • 常数项可以忽略，所以复杂度是 O(2^n)

这个函数的问题在于：太多重复调用，很多重复计算，比如执行了多次 fib(1), fib(2) 等等。

2、现在分析 fib(2) 函数

	// O(n)
	public static int fib2(int n) { // 非递归
		if (n <= 1) return n;
		
		int first = 0;
		int second = 1;
		for (int i = 0; i < n - 1; i++) {
			int sum = first + second;
			first = second;
			second = sum;
		}
		return second;
	}

// 另一种写法
	public static int fib2(int n) { // 非递归
		if (n <= 1) return n;
		
		int first = 0;
		int second = 1;
		while (n-- > 1) {
		  second = first + second;
			first = second - first;
		}
		return second;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
  • 总执行次数 = 1 + (n-1) + (n-1) + (n-1) = 3n - 2
  • 所以复杂度为 O(n)

总结

fib2 函数性能远高于 fib1

有时候算法之间的差距，往往比硬件方面的差距还要大

# 算法的优化方向

  1. 用尽量少的存储空间
  2. 用尽量少的执行步骤（执行时间）
  3. 根据情况，可以
    • 空间换时间
    • 时间换空间

具体来说：

  1. 空间优化：
    • 减少数据结构的空间占用：使用紧凑的数据结构来存储数据，例如使用位压缩或哈希表来减少内存占用。
    • 避免不必要的副本：在算法中尽量避免复制数据，而是通过引用来共享数据，以节省内存。
    • 内存分配的优化：减少内存分配次数，可以使用对象池或缓存来重复使用已分配的内存，减少垃圾回收的开销。
  2. 时间优化：
    • 减少循环迭代次数：尽量减少循环的迭代次数，可以通过使用更高效的算法来实现。
    • 使用数据结构的高效方法：了解数据结构的内部实现和方法的复杂度，选择最适合问题的数据结构和算法。
    • 并行化和异步化：将计算任务分解为多个子任务，并行执行，以提高性能。
    • 算法复杂度的优化：通过改进算法本身来降低时间复杂度，例如从 O(n^2) 降低到 O(n log n)。
  3. 时间与空间权衡：
    • 空间换时间：有时可以通过使用额外的内存来加速算法，例如使用缓存来存储计算结果，以减少重复计算的开销。
    • 时间换空间：在内存受限的情况下，可以通过牺牲一些计算时间来降低内存占用，例如对大型数据集进行分页处理而不是一次性加载所有数据。

以下是一些示例：

  • 空间优化：
    • 位图压缩：对大规模布尔型数据进行压缩，用较少的内存存储。
    • 内存映射文件：通过内存映射文件技术，将大文件映射到虚拟内存，避免了读取整个文件到内存的开销。
  • 时间优化：
    • 快速排序算法：相比于冒泡排序，快速排序具有更好的平均时间复杂度，通常用于排序大数据集。
    • 哈希表查找：使用哈希表来实现 O(1) 时间复杂度的查找操作。
  • 时间与空间权衡：
    • 缓存：使用缓存来存储频繁访问的数据，以减少数据库查询或计算的时间。
    • 分段加载：将大型文件或数据集分为多个片段，按需加载，减少内存占用。

总之，算法的优化方向应该根据具体问题和性能需求来确定。通常需要进行权衡，以找到最合适的解决方案。同时，优化不应该牺牲代码的可读性和维护性，需要综合考虑多个因素。

# 力扣 - 斐波那契数

地址：509. 斐波那契数 - 力扣（LeetCode） (opens new window)

# 复杂度的三种情况

  1. 最好情况复杂度
  2. 最坏情况复杂度
  3. 平均情况复杂度

# 总结

复杂度是衡量算法执行效率的一种度量标准。

它用于描述算法在处理输入数据时所需的资源量，通常以时间复杂度和空间复杂度两个方面进行评估。

  • 时间复杂度：时间复杂度衡量算法执行所需的时间资源，通常用大 O 表示法表示。它表示算法运行时间与输入规模之间的关系。常见的时间复杂度包括：
    1. 常数时间复杂度（O(1)）：无论输入规模大小，算法的执行时间都是恒定的。
    2. 线性时间复杂度（O(n)）：算法的执行时间与输入规模成线性关系。
    3. 对数时间复杂度（O(log n)）：算法的执行时间与输入规模的对数成关系。
    4. 平方时间复杂度（O(n^2)）：算法的执行时间与输入规模的平方成关系。
    5. 指数时间复杂度（O(2^n)）：算法的执行时间与输入规模的指数成关系。
  • 空间复杂度：空间复杂度衡量算法执行所需的内存资源。它表示算法所需的额外空间与输入规模之间的关系。常见的空间复杂度包括：
    1. 常数空间复杂度（O(1)）：算法执行所需的额外空间是恒定的。
    2. 线性空间复杂度（O(n)）：算法执行所需的额外空间与输入规模成线性关系。
    3. 对数空间复杂度（O(log n)）：算法执行所需的额外空间与输入规模的对数成关系。
上次更新: 2024/9/25 11:16:13
学前须知
动态数组

← 动态数组→

Theme by Vdoing | Copyright © 2023-2024 沉梦听雨 | MIT License