计算机基础
数据结构与算法
力扣篇
Hot100题解

中等篇（中）

# 中等篇（中）

# 53. 最大子数组和 (opens new window)

# 题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

1
2
3

示例 2：

输入：nums = [1]
输出：1

1
2

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

1
2

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104

**进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

# 方法一：动态规划

    /**
     * 1、动态规划 -- 1ms(100.00%), 58.52MB(10.57%)
     * <p>
     * 时间复杂度为：O(n)，代码只包含一个循环，该循环遍历了数组中的每个元素一次。
     * <p>
     * 空间复杂度为：O(1)，因为代码中只使用了常量级的额外空间，不随输入规模变化。
     */
    class Solution {
        public int maxSubArray(int[] nums) {
            int n = nums.length;

            // 初始化 最大子数组和
            int maxSum = nums[0];
            // 初始化 当前子数组和
            int currentSum = nums[0];

            // 从第二个元素开始遍历
            for (int i = 1; i < n; i++) {
                // 更新子数组和，当前子数组和等于 当前元素 和 当前子数组和 中的最大值
                currentSum = Math.max(nums[i], currentSum + nums[i]);
                // 更新最大子数组和
                maxSum = Math.max(maxSum, currentSum);
            }

            return maxSum;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 方法二：分治法

最大子数组问题可以使用分治法来求解。

分治法的基本思想是：将问题分解成更小的子问题，解决子问题后再合并得到原问题的解。

对于最大子数组问题，可以采用如下的分治策略：

分解（Divide）： 将数组分成两半，分别求解左半部分和右半部分的最大子数组和。
合并（Combine）： 考虑最大子数组和跨越左右两半的情况。即求解包含中间元素的最大子数组和。
返回（Return）： 返回左半部分、右半部分和跨越中间的最大子数组和中的最大值。

    /**
     * 2、分治法 -- 12ms(5.40%), 58.3MB(15.58%)
     * <p>
     * 时间复杂度为：O(nlogn)。
     * <p>
     * 空间复杂度为：O(logn)。
     */
    class Solution {
        public int maxSubArray(int[] nums) {
            // if (nums == null || nums.length == 0) {
            //     return 0;
            // }

            return divideAndConquer(nums, 0, nums.length - 1);
        }

        private int divideAndConquer(int[] nums, int left, int right) {
            if (left == right) {
                return nums[left];
            }

            int mid = (left + right) / 2;

            // 分别求解左右两半的最大子数组和
            int leftMax = divideAndConquer(nums, left, mid);
            int rightMax = divideAndConquer(nums, mid + 1, right);

            // 求解跨越中间的最大子数组和
            int crossMax = maxCrossingSubarray(nums, left, mid, right);

            // 返回左半部分、右半部分和跨越中间的最大子数组和中的最大值
            return Math.max(Math.max(leftMax, rightMax), crossMax);
        }

        private int maxCrossingSubarray(int[] nums, int left, int mid, int right) {
            int leftMax = Integer.MIN_VALUE;
            int sum = 0;

            // 从中间元素向左计算最大子数组和
            for (int i = mid; i >= left; i--) {
                sum += nums[i];
                leftMax = Math.max(leftMax, sum);
            }

            int rightMax = Integer.MIN_VALUE;
            sum = 0;

            // 从中间元素向右计算最大子数组和
            for (int i = mid + 1; i <= right; i++) {
                sum += nums[i];
                rightMax = Math.max(rightMax, sum);
            }

            // 返回跨越中间的最大子数组和
            return leftMax + rightMax;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

# 代码解析

maxSubArray 方法调用 divideAndConquer 方法进行递归求解。
divideAndConquer 方法分别对左半部分、右半部分和跨越中间的情况进行递归求解，然后返回三者中的最大值。
maxCrossingSubarray 方法用于求解跨越中间的最大子数组和。

# 分治法复杂度分析

时间复杂度：
- 在每一次递归调用中，数组被均匀地分成两半。
- 每一层的工作量是线性的，因为在每一次递归调用中，我们需要线性时间计算跨越中间的最大子数组和。
- 因此，总体的时间复杂度是 O(n log n)，其中 n 是数组的长度。
空间复杂度：
- 在每次递归调用中，需要一定的栈空间，但由于这是一个尾递归形式，所以整个递归过程所需要的栈空间是 O(log n)。
- 因此，总体的空间复杂度是 O(log n)。

# 54. 螺旋矩阵 (opens new window)

# 题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

1
2

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

1
2

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

# 方法一：模拟

# 思路分析

初始化四个边界 top、bottom、left、right。
在一个循环中，依次从左到右、从上到下、从右到左、从下到上遍历矩阵。
在每次遍历过程中，更新相应的边界，并将对应位置的元素添加到结果列表中。
循环直到某一边界超过了另一边界。

# 代码实现

    /**
     * 1、使用两个标记数组：额外空间 O(m + n) -- 0ms(100.00%), 40.5MB(5.5%)
     * <p>
     * 时间复杂度：O(m * n)，其中 m 为矩阵的行数，n 为矩阵的列数。
     * <p>
     * 空间复杂度：O(1)，使用了两个额外的数组。
     */
    class Solution {
        public List<Integer> spiralOrder(int[][] matrix) {
            List<Integer> result = new ArrayList<>();
            if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
                return result;
            }

            int top = 0, bottom = matrix.length - 1, left = 0, right = matrix[0].length - 1;

            while (top <= bottom && left <= right) {
                // 从左到右
                for (int i = left; i <= right; i++) {
                    result.add(matrix[top][i]);
                }
                top++;

                // 从上到下
                for (int i = top; i <= bottom; i++) {
                    result.add(matrix[i][right]);
                }
                right--;

                // 从右到左
                if (top <= bottom) {
                    for (int i = right; i >= left; i--) {
                        result.add(matrix[bottom][i]);
                    }
                    bottom--;
                }

                // 从下到上
                if (left <= right) {
                    for (int i = bottom; i >= top; i--) {
                        result.add(matrix[i][left]);
                    }
                    left++;
                }
            }

            return result;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 方法二：模拟（巧妙且紧凑）

# 代码实现

    /**
     * 2、模拟，作者：Krahets -- 0ms(100.00%), 40.4MB(5.5%)
     * 原文链接：https://leetcode.cn/problems/spiral-matrix/solutions/2362055/54-luo-xuan-ju-zhen-mo-ni-qing-xi-tu-jie-juvi/
     * <p>
     * 时间复杂度：O(m * n)，其中 m 为矩阵的行数，n 为矩阵的列数。
     * <p>
     * 空间复杂度：O(1)，使用常量空间。
     */
    class Solution2 {
        public List<Integer> spiralOrder(int[][] matrix) {
            if (matrix.length == 0)
                return new ArrayList<Integer>();
            int l = 0, r = matrix[0].length - 1, t = 0, b = matrix.length - 1, x = 0;
            Integer[] res = new Integer[(r + 1) * (b + 1)];
            while (true) {
                for (int i = l; i <= r; i++) res[x++] = matrix[t][i]; // left to right
                if (++t > b) break;
                for (int i = t; i <= b; i++) res[x++] = matrix[i][r]; // top to bottom
                if (l > --r) break;
                for (int i = r; i >= l; i--) res[x++] = matrix[b][i]; // right to left
                if (t > --b) break;
                for (int i = b; i >= t; i--) res[x++] = matrix[i][l]; // bottom to top
                if (++l > r) break;
            }
            return Arrays.asList(res);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 算法分析

解法的主要步骤：

初始化四个边界，l、r、t、b 分别表示当前遍历的左、右、上、下边界。
使用 x 记录遍历的位置，同时初始化一个大小为矩阵总元素个数的数组 res 用于保存遍历结果。
在一个循环中，首先从左到右遍历上边界，然后从上到下遍历右边界，接着从右到左遍历下边界，最后从下到上遍历左边界。
在每次遍历边界的过程中，将对应位置的元素放入 res 数组中，并更新边界。
循环直到某一个边界超过了另一个边界，表示遍历完成。

# 56. 合并区间 (opens new window)

# 题目描述

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

1
2
3

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

1
2
3

提示：

1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104

# 方法一：排序 + 一次遍历

思路分析

首先对输入的区间按照起始值进行排序，
然后遍历排序后的区间，检查每个区间是否与结果列表中的最后一个区间重叠。
- 如果重叠，则通过更新最后一个区间的结束值来合并区间；
- 如果不重叠，则将当前区间添加到结果列表中。
最后，将结果列表转换为二维数组并返回。

代码

class Solution {
        public int[][] merge(int[][] intervals) {
            // 1、根据起始值对区间进行排序（快速排序）
            Arrays.sort(intervals, (a, b) -> a[0] - b[0]);

            // 2、初始化列表以存储合并后的区间
            List<int[]> res = new ArrayList<>();

            // 3、将第一个区间添加到结果列表中
            // 假设为 [a, b]
            res.add(intervals[0]);

            // 4、遍历排序后的区间
            for (int i = 1; i < intervals.length; i++) {
                // 假设为 [c, d]
                int start = intervals[i][0], end = intervals[i][1];

                // 4.1、检查当前区间是否与结果列表中的最后一个区间重叠
                if (res.get(res.size() - 1)[1] < start) { 
                    // 此时 b < c
                    // 4.1.1、如果不重叠，则将当前区间添加到结果列表中
                    res.add(intervals[i]);
                } else { 
                    // 此时 b >= c, (b > d 或者 b = d 或者 b < d), 所以要以最大值更新
                    // 4.1.2、如果重叠，则通过更新最后一个区间的结束值来合并区间
                    res.get(res.size() - 1)[1] = Math.max(res.get(res.size() - 1)[1], end);
                }
            }

            // 5、将列表转换为二维数组并返回
            return res.toArray(new int[res.size()][]);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 复杂度分析

时间复杂度：
- 排序操作的时间复杂度为 O(nlogn)，其中 n 为区间的数量。
- 遍历操作的时间复杂度为 O(n)。
- 因此，整段代码的时间复杂度为 O(nlogn)。
空间复杂度：
- 因为在排序过程中，使用了快速排序算法，其空间复杂度为 O(logn)。
- 而遍历操作的空间复杂度为 O(1)。
- 因此，整段代码的空间复杂度为 O(logn)。

# 73. 矩阵置零 (opens new window)

# 题目描述

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 (opens new window) 算法**。**

示例 1：

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

1
2

示例 2：

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

1
2

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

进阶：

一个直观的解决方案是使用 O(*m**n*) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(*m* + *n*) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

# 方法一：使用两个标记数组

    /**
     * 1、使用两个标记数组：额外空间 O(m + n) -- 0ms(100.00%), 51.84MB(9.51%)
     * <p>
     * 时间复杂度：O(m * n)，其中 m 为矩阵的行数，n 为矩阵的列数。
     * <p>
     * 空间复杂度：O(m + n)，使用了两个额外的数组。
     */
    class Solution {
        public void setZeroes(int[][] matrix) {
            int m = matrix.length;
            int n = matrix[0].length;
            boolean[] rows = new boolean[m];
            boolean[] cols = new boolean[n];

            // 遍历矩阵，记录包含 0 的行和列
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (matrix[i][j] == 0) {
                        rows[i] = true;
                        cols[j] = true;
                    }
                }
            }

            // 再次遍历矩阵，根据记录的信息将元素置为 0
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (rows[i] || cols[j]) {
                        matrix[i][j] = 0;
                    }
                }
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 方法二：使用常量空间的原地算法

# 算法分析

首行和首列标记零元素：
- 遍历整个矩阵，如果当前元素 matrix[i][j] 是零，就将该元素所在的首行和首列的元素置零。
- 同时用两个布尔变量 firstRowHasZero 和 firstColHasZero 记录首行和首列是否包含零。
根据首行和首列的标记，将元素置为零：
- 遍历整个矩阵，如果首行或首列的对应元素是零，就将当前元素置零。
处理首行和首列：
- 如果 firstRowHasZero 为真，将首行所有元素置零。
- 如果 firstColHasZero 为真，将首列所有元素置零。

这样，通过两轮遍历和标记，该算法就能够在常量空间内完成矩阵的原地修改，将包含零元素的行和列都置零。

# 代码

    /**
     * 2、使用常量空间的原地算法
     * <p>
     * 时间复杂度：O(m * n)，其中 m 为矩阵的行数，n 为矩阵的列数。
     * <p>
     * 空间复杂度：O(1)，使用常量空间。
     */
    class Solution {
        public void setZeroes(int[][] matrix) {
            int m = matrix.length;
            int n = matrix[0].length;
            boolean firstRowHasZero = false;
            boolean firstColHasZero = false;

            // 用首行和首列标记是否包含 0
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (matrix[i][j] == 0) {
                        // 如果当前元素是 0，将首行和首列【对应】的元素置为 0
                        if (i == 0) firstRowHasZero = true;
                        if (j == 0) firstColHasZero = true;
                        matrix[i][0] = matrix[0][j] = 0;
                    }
                }
            }

            // 根据首行和首列的标记，将元素置为 0
            for (int i = 1; i < m; i++) {
                for (int j = 1; j < n; j++) {
                    if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                        matrix[i][j] = 0;
                    }
                }
            }

            // 处理首行和首列
            if (firstRowHasZero) {
                for (int j = 0; j < n; j++) {
                    matrix[0][j] = 0;
                }
            }

            if (firstColHasZero) {
                for (int i = 0; i < m; i++) {
                    matrix[i][0] = 0;
                }
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 98. 验证二叉搜索树 (opens new window)

# 题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

1
2

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

1
2
3

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

# 方法一：递归

    /**
     * 1、递归 -- 0ms(100.00%), 42.29MB(79.61%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        // 定义一个 long 类型的变量 pre，初始值为 Long.MIN_VALUE
        long pre = Long.MIN_VALUE;

        public boolean isValidBST(TreeNode root) {
            // 如果传入的 root 节点为空，则返回 true
            if (root == null) {
                return true;
            }
            // 如果左子树不为空，则递归判断左子树是否为二叉搜索树
            if (!isValidBST(root.left)) {
                return false;
            }
            // 如果当前节点的值小于等于 pre，则返回 false
            if (root.val <= pre) {
                return false;
            }
            // 否则，将当前节点的值赋值给 pre
            pre = root.val;
            // 递归判断右子树是否为二叉搜索树
            return isValidBST(root.right);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 42.05MB(91.85%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solutio2 {
        public boolean isValidBST(TreeNode root) {
            // 调用dfs函数，传入root节点，以及long类型的最小值和最大值
            return dfs(root, Long.MIN_VALUE, Long.MAX_VALUE);
        }

        // 定义一个dfs函数，用来递归判断node节点是否在给定的范围内
        private boolean dfs(TreeNode root, long l, long r) {
            // 如果node为空，则返回true
            if (root == null) {
                return true;
            }
            // 如果node的值小于等于左边界或者大于等于右边界，则返回false
            if (root.val <= l || root.val >= r) {
                return false;
            }
            // 递归调用dfs函数，传入node的左节点和右节点，以及边界值l和r
            return dfs(root.left, l, root.val) && dfs(root.right, root.val, r);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 102. 二叉树的层序遍历 (opens new window)

# 题目描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

1
2

示例 2：

输入：root = [1]
输出：[[1]]

1
2

示例 3：

输入：root = []
输出：[]

1
2

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

# 方法一：队列实现层序遍历

    /**
     * 1、队列实现层序遍历 -- 1ms(92.39%), 43.83MB(16.72%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public List<List<Integer>> levelOrder(TreeNode root) {
            List<List<Integer>> res = new ArrayList<>();
            if (root == null) {
                return res;
            }
            Queue<TreeNode> queue = new ArrayDeque<>();
            queue.offer(root);

            while (!queue.isEmpty()) {
                int size = queue.size();
                List<Integer> ele = new ArrayList<>();

                while (size > 0) {
                    TreeNode cur = queue.poll();
                    ele.add(cur.val);
                    if (cur.left != null) {
                        queue.offer(cur.left);
                    }
                    if (cur.right != null) {
                        queue.offer(cur.right);
                    }
                    size--;
                }

                res.add(ele);
            }

            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 44.04MB(5.15%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        List<List<Integer>> res = new ArrayList<>();

        public List<List<Integer>> levelOrder(TreeNode root) {
            dfs(root, 0);
            return res;
        }

        public void dfs(TreeNode node, int deep) {
            if (node == null) {
                return;
            }
            if (res.size() < deep + 1) {
                res.add(new ArrayList<>());
            }
            res.get(deep).add(node.val);
            dfs(node.left, deep + 1);
            dfs(node.right, deep + 1);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 105. 从前序与中序遍历序列构造二叉树 (opens new window)

# 题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

1
2

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

1
2

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

# 方法一：哈希表 + 递归

    /**
     * 1、哈希表 + 递归 -- 1ms(98.94%), 43.15MB(59.30%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        private int[] preorder; // 存储前序遍历的结果
        private Map<Integer, Integer> indexMap = new HashMap<>(); // 存储中序遍历结果的值到索引的映射

        // 输入前序遍历和中序遍历的结果，构建并返回二叉树
        public TreeNode buildTree(int[] preorder, int[] inorder) {
            int length = preorder.length; // 树的节点数量
            this.preorder = preorder; // 存储前序遍历结果到成员变量
            // 存储中序遍历结果的值和索引，映射到 indexMap
            for (int i = 0; i < length; i++) {
                indexMap.put(inorder[i], i);
            }
            // 构建整棵树并返回 -- dfs(i,j,n)，其中之和j分别表示前序序列和中序序列的起始位置，而n表示节点个数
            return buildSubTree(0, 0, length);
        }

        /**
         * 根据前序和中序遍历的结果构建子树
         *
         * @param rootIndexPreorder 在前序遍历序列中当前子树的根节点的索引 -- 前序序列的起始位置
         * @param leftIndexInorder 在中序遍历序列中当前子树的最左节点的索引 -- 中序序列的起始位置
         * @param subTreeSize 当前子树的节点数量
         * @return
         */
        private TreeNode buildSubTree(int rootIndexPreorder, int leftIndexInorder, int subTreeSize) {
            // 子树没有节点，返回 null
            if (subTreeSize <= 0) {
                return null;
            }
            // 找到 根节点的值 和 在中序遍历结果中的索引
            int rootValue = preorder[rootIndexPreorder];
            int rootIndexInorder = indexMap.get(rootValue);
            // 构建左子树
            TreeNode leftSubTree = buildSubTree(rootIndexPreorder + 1,
                    leftIndexInorder,
                    rootIndexInorder - leftIndexInorder);
            // 构建右子树
            TreeNode rightSubTree = buildSubTree(rootIndexPreorder + 1 + rootIndexInorder - leftIndexInorder,
                    rootIndexInorder + 1,
                    subTreeSize - 1 - (rootIndexInorder - leftIndexInorder) );
            // 构建当前节点并返回
            return new TreeNode(rootValue, leftSubTree, rightSubTree);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

整体思路是，

通过前序遍历的结果确定当前子树的根节点，然后在中序遍历的结果中找到根节点的位置，进而划分左子树和右子树。递归调用这个过程，直到子树的节点数量为 0 时返回 null。

# 方法二：递归

    /**
     * 2、递归 -- 0ms(100.00%), 43.30MB(38.06%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        // 全局变量 pre 和 in 用于追踪前序遍历和中序遍历的位置
        public int pre = 0;
        public int in = 0;

        // 主方法，入口点，接收前序遍历和中序遍历的结果，返回构建的二叉树的根节点
        public TreeNode buildTree(int[] preorder, int[] inorder) {
            // 调用深度优先搜索方法，并传入 stop 参数作为中序遍历的停止条件
            return dfs(preorder, inorder, 3001);
        }

        // 深度优先搜索方法，根据前序遍历和中序遍历的结果构建二叉树
        public TreeNode dfs(int[] preorder, int[] inorder, int stop) {
            // 如果前序遍历已经遍历完，返回 null
            if (pre == preorder.length) {
                return null;
            }
            // 如果中序遍历的当前节点的值等于停止条件，表示当前子树的左子树已经构建完毕
            if (inorder[in] == stop) {
                in++;
                return null; // 返回 null 表示当前节点的左子树为空
            }
            // 构建当前节点，节点值为前序遍历的当前位置的值
            TreeNode node = new TreeNode(preorder[pre++]);
            // 递归构建左子树，停止条件为当前节点的值
            node.left = dfs(preorder, inorder, node.val);
            // 递归构建右子树，停止条件为传入的停止条件
            node.right = dfs(preorder, inorder, stop);
            // 返回当前节点
            return node;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# 114. 二叉树展开为链表 (opens new window)

# 题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 (opens new window) 顺序相同。

示例 1：

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

1
2

示例 2：

输入：root = []
输出：[]

1
2

示例 3：

输入：root = [0]
输出：[0]

1
2

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

# 方法一：寻找前驱节点

    /**
     * 1、寻找前驱节点 -- 0ms(100.00%), 41.00MB(55.78%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution {
        public void flatten(TreeNode root) {
            while (root != null) {
                if (root.left != null) {
                    // 找到当前节点左子树的最右节点
                    TreeNode pre = root.left;
                    while (pre.right != null) {
                        pre = pre.right;
                    }

                    // 将左子树的最右节点（前驱节点）指向原来的右子树
                    pre.right = root.right;

                    // 将当前节点的右节点指向左子树
                    root.right = root.left;
                    root.left = null;
                }
                root = root.right;
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 128. 最长连续序列 (opens new window)

# 题目描述

    /* 给定一个未排序的整数数组 nums，
       找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。
       请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 */

1
2
3

# 方法一：排序

    /**
     * 1、排序 -- 12ms(95.50%), 55.59MB(61.59%)
     * <p>
     * 时间复杂度为 O(n * logn)
     * 空间复杂度为 O(logn)
     */
    class Solution {
        public int longestConsecutive(int[] nums) {
            int len = nums.length;
            if (len < 2) {
                return len;
            }

            // 对数组进行排序
            Arrays.sort(nums);
            // 最长序列
            int res = 0;
            // 当前连续序列长度
            int sum = 0;

            // 遍历数组
            for (int i = 0; i < len; i++) {

                // 如果当前元素和下一个元素差1，则sum+1，更新res
                if ((i + 1) < len && nums[i + 1] == (nums[i] + 1)) {
                    sum += 1;
                    res = Math.max(res, sum);
                    // 如果当前元素和下一个元素相等，则跳过
                } else if ((i + 1) < len && nums[i + 1] == (nums[i])) {
                    continue;
                    // 如果当前元素和下一个元素不相等，则sum+1，更新res
                } else {
                    sum += 1;
                    res = Math.max(res, sum);
                    // 重置sum
                    sum = 0;
                }
            }

            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# 方法二：哈希表

    /**
     * 2、哈希表官方题解 -- -- 25ms(77.71%), 60.17MB(27.24%)
     * <p>
     * 时间复杂度为 O(n)
     * 空间复杂度为 O(n)
     */
   class Solution {
        public int longestConsecutive(int[] nums) {
            // 创建一个HashSet，用于存储数组中的元素
            Set<Integer> num_set = new HashSet<Integer>();
            // 遍历数组，将数组中的元素添加到HashSet中
            for (int num : nums) {
                num_set.add(num);
            }

            // 定义一个变量，用于存储最长连续序列的长度
            int longestStreak = 0;

            // 遍历HashSet，查找连续序列的最大长度
            for (int num : num_set) {
                // 如果HashSet中不包含num-1，则表示当前元素是连续序列的第一个元素
                if (!num_set.contains(num - 1)) {
                    // 定义一个变量，用于存储当前连续序列的长度
                    int currentNum = num;
                    int currentStreak = 1;

                    // 遍历当前元素，查找连续序列的最大长度
                    while (num_set.contains(currentNum + 1)) {
                        currentNum += 1;
                        currentStreak += 1;
                    }

                    // 将当前连续序列的长度与最长连续序列的长度进行比较，取最大值
                    longestStreak = Math.max(longestStreak, currentStreak);
                }
            }

            // 返回最长连续序列的长度
            return longestStreak;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

# 138. 随机链表的复制 (opens new window)

# 题目描述

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝 (opens new window)。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

示例 1：

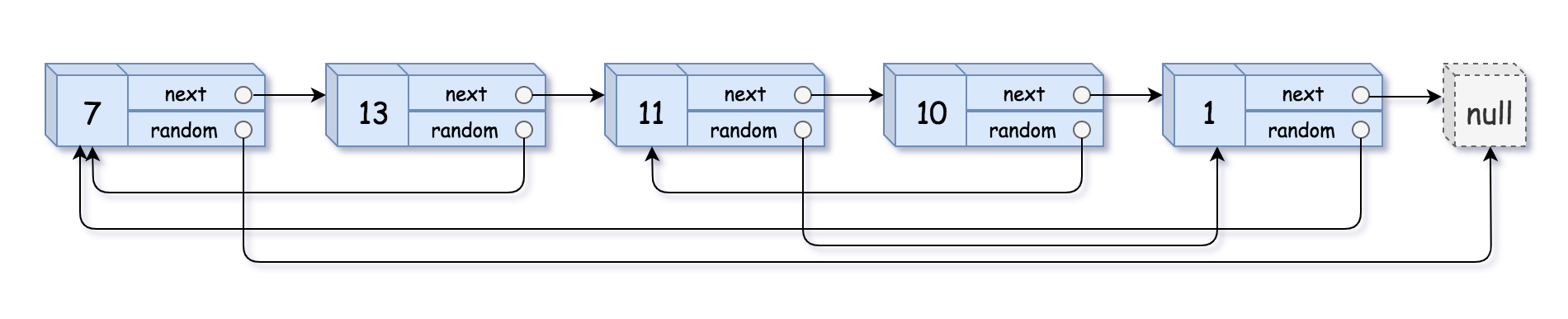
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

1
2

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

1
2

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

1
2

提示：

0 <= n <= 1000
-104 <= Node.val <= 104
Node.random 为 null 或指向链表中的节点。

复制带有随机指针的链表

# 方法一：哈希表

    /**
     * 1、哈希表 -- 0ms(100.00%), 43.09MB(26.26%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(n)
     */
    class Solution {
        public Node copyRandomList(Node head) {
            // 如果原链表头节点为空，返回空
            if (head == null) {
                return null;
            }

            // 创建当前节点 cur，并初始化为原链表头节点
            Node cur = head;
            // 创建一个映射表 map，用于存储原链表节点和新链表节点的对应关系
            Map<Node, Node> map = new HashMap<>();

            // 第一遍循环，创建新链表节点并将其存入映射表
            while (cur != null) {
                // 将当前节点 cur 作为 key，创建一个值为当前节点值的新节点作为 value 放入映射表
                map.put(cur, new Node(cur.val));
                // 将当前节点指针 cur 移动到下一个节点
                cur = cur.next;
            }

            // 将当前节点 cur 重新指向原链表头节点
            cur = head;
            // 第二遍循环，连接新链表的 next 和 random 指针
            while (cur != null) {
                // 通过映射表获取当前节点 cur 对应的新节点，然后设置新节点的 next 和 random 指针
                map.get(cur).next = map.get(cur.next);
                map.get(cur).random = map.get(cur.random);
                // 将当前节点指针 cur 移动到下一个节点
                cur = cur.next;
            }

            // 返回新链表的头节点
            return map.get(head);
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

注释：

在第一次循环中，创建一个新链表，并将原链表节点和新链表节点的对应关系存入映射表。
在第二次循环中，通过映射表连接新链表的 next 和 random 指针。
最后返回新链表的头节点。

# 方法二：拼接 + 拆分

    /**
     * 2、拼接 + 拆分 -- 0ms(100.00%), 43.25MB(17.02%)
     * <p>
     * 时间复杂度：O(n)
     * <p>
     * 空间复杂度：O(1)
     */
    class Solution2 {
        public Node copyRandomList(Node head) {
            // 如果原链表头节点为空，返回空
            if (head == null) {
                return null;
            }

            // 第一遍循环，在每个节点后面插入一个相同值的新节点
            Node cur = head;
            while (cur != null) {
                // 创建一个新节点 tmp，值为当前节点的值
                Node tmp = new Node(cur.val);
                // 将新节点的 next 指针指向当前节点的下一个节点
                tmp.next = cur.next;
                // 将当前节点的 next 指针指向新节点
                cur.next = tmp;
                // 将当前节点指针 cur 移动到下一个节点的下一个节点
                cur = tmp.next;
            }

            // 第二遍循环，连接新节点的 random 指针
            cur = head;
            while (cur != null) {
                // 如果当前节点的 random 指针不为空，将新节点的 random 指针指向当前节点 random 指针的下一个节点
                if (cur.random != null) {
                    cur.next.random = cur.random.next;
                }
                // 将当前节点指针 cur 移动到下一个节点的下一个节点
                cur = cur.next.next;
            }

            // 第三遍循环，分离新旧链表
            cur = head.next;
            Node pre = head, res = head.next;
            while (cur.next != null) {
                // 将原链表的 next 指针指向下一个节点的下一个节点
                pre.next = pre.next.next;
                // 将新链表的 next 指针指向下一个节点的下一个节点
                cur.next = cur.next.next;
                // 将原链表和新链表的指针分别移动到下一个节点
                pre = pre.next;
                cur = cur.next;
            }
            // 将原链表的尾部节点的 next 指针置为空
            pre.next = null;
            // 返回新链表的头节点
            return res;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

注释：

采用了三次遍历的方法。

第一遍循环，在每个节点后面插入一个相同值的新节点。
第二遍循环，连接新节点的 random 指针。
第三遍循环，分离原链表和新链表。

参考文章：138. 随机链表的复制 - 力扣（LeetCode） (opens new window)

上次更新: 2024/9/25 11:16:13

← 中等篇（上）中等篇（下）→